Review Căn 3 bình phương bằng bao nhiêu?
Thủ Thuật về Căn 3 bình phương bằng bao nhiêu? Chi Tiết
An Sơn Hà đang tìm kiếm từ khóa Căn 3 bình phương bằng bao nhiêu? được Cập Nhật vào lúc : 2022-12-21 02:02:05 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Mình lý giải và hướng dẫn lại nha.Cho số dương "a", căn bậc hai của "a", ký hiệu là a, là số dương "b" sao cho khi "b" được nhân với cùng, kết quả là "a".
Nội dung chính Show- Căn bậc 3Chúng ta hoàn toàn có thể tìm thấy số 3 ở đâu?3 một số trong những vô tỷĐồ thị và công thứcMáy tính giải khai căn bậc 3 OnlineHãy đưa ra 1 giá trị3 bình phương bằng bao nhiêu?Căn A bình phương bằng bao nhiêu?1 bình phương bằng bao nhiêu?3 căn 8 bằng bao nhiêu?
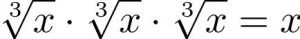
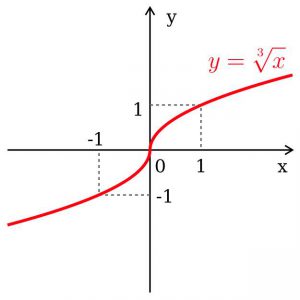
Đồ thị và công thức
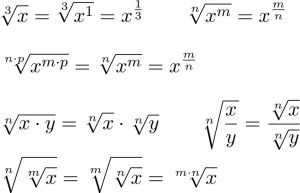
Máy tính giải khai căn bậc 3 Online
Hãy đưa ra 1 giá trị
x ==Làm tròn số thập phân
- share share
Trong chương trình lớp 9 , những kì thi vào 10 hay thi HSG toán 9 thường có những bài toán về khai triển căn bậc 3 dạng $sqrt[3]a+sqrtb$ trong đó a,b nguyên cho trước (b$geq$0). Cuối cùng sẽ phân tích biểu thức trong căn về căn bậc 3 dạng ($c+sqrtd$)$^3$ để khai căn bậc 3 ( c,d nguyên chưa chắc như đinh , d>0 )
Vậy ta sẽ tìm c,d = CASIO:
Giả sử $sqrt[3]a+sqrtb$=$sqrt[3](c+sqrtd)^3$=$c+sqrtd$
Mặt khác $sqrt[3](c+sqrtd)^3$=$sqrt[3]c^3+3cd+(3c^2+d)sqrtd$
Do c,d nguyên nên $c^3+3cd$ nguyên
Vậy phải tìm c,d tm hệ $left{beginmatrixc^3+3cd=a & \ c+sqrtd= sqrt[3]a+sqrtb& endmatrixright.$
Tức là phải giải phương trình : $3c(sqrt[3]a+sqrtb-c)^2+c^3=a$
Vậy là quy về phương trình 1 ẩn c vì a,b biết trước rồi
Bấm biểu thức trên vào máy tính casio, giải ra được c
Tìm d bằng phương pháp bấm $sqrt[3]a+sqrtb-c=$ , được $sqrtd$ .
Bấm Ans$^2$ ta được d .
Nói chung là chỉ việc nhớ cái pt ở đầu cuối là được . Cái này chỉ áp dụng cho những căn bậc 3 mà bản thân nó hoàn toàn có thể viết được thôi .
Còn về căn bậc 2 ta cũng hoàn toàn có thể làm kiểu này , nhưng thuận tiện và đơn giản hơn nhiều . Các bạn thử xem !
Bài viết đã được sửa đổi nội dung bởi etucgnaohtn: 11-05-2013 - 19:46
Trong chương trình lớp 9 , những kì thi vào 10 hay thi HSG toán 9 thường có những bài toán về khai triển căn bậc 3 dạng $sqrt[3]a+sqrtb$ trong đó a,b nguyên cho trước (b$geq$0). Cuối cùng sẽ phân tích biểu thức trong căn về căn bậc 3 dạng ($c+sqrtd$)$^3$ để khai căn bậc 3 ( c,d nguyên chưa chắc như đinh , d>0 )
Vậy ta sẽ tìm c,d = CASIO:
Giả sử $sqrt[3]a+sqrtb$=$sqrt[3](c+sqrtd)^3$=$c+sqrtd$
Mặt khác $sqrt[3](c+sqrtd)^3$=$sqrt[3]c^3+3cd+(3c^2+d)sqrtd$
Do c,d nguyên nên $c^3+3cd$ nguyên
Vậy phải tìm c,d tm hệ $left{beginmatrixc^3+3cd=a & \ c+sqrtd= sqrt[3]a+sqrtb& endmatrixright.$
Tức là phải giải phương trình : $3c(sqrt[3]a+sqrtb-c)^2+c^3=a$
Vậy là quy về phương trình 1 ẩn c vì a,b biết trước rồi
Bấm biểu thức trên vào máy tính casio, giải ra được c
Tìm d bằng phương pháp bấm $sqrt[3]a+sqrtb-c=$ , được $sqrtd$ .
Bấm Ans$^2$ ta được d .
Nói chung là chỉ việc nhớ cái pt ở đầu cuối là được . Cái này chỉ áp dụng cho những căn bậc 3 mà bản thân nó hoàn toàn có thể viết được thôi .
Còn về căn bậc 2 ta cũng hoàn toàn có thể làm kiểu này , nhưng thuận tiện và đơn giản hơn nhiều . Các bạn thử xem !
Thế này nhé ! Mình có một cách không khoa học nhưng hiệu suất cao, bạn tham khảo :
$A=sqrt[3]44+18sqrt6$
Nhận xét rằng A phải viết được dưới dạng $A=sqrt[3](a+b)^3Rightarrow A^3=(a+b)^3=a(a^2+3b^2)+b(b^2+3a^2)Rightarrow 44+18sqrt6=a(a^2+3b^2)+b(b^2+3a^2)$
Ta cứ lấy giá trị sau :
$18sqrt6=a(a^2+3b^2)Rightarrow left{beginmatrix & a=sqrt6 & \ & a^2+3b^2=18 & endmatrixright. Rightarrow $a=sqrt6;b=2$
Suy ra $A=2+sqrt6$
Với trường hợp ta làm như trên mà không tìm được a;b "đẹp" thì hoàn toàn có thể nhân 2, nhân 3 vào biểu thức A
Thi MTCT tỉnh Đồng Nai năm nay cũng luôn có thể có một câu thế này, nhờ cách này mà mình làm được đấy !
Bài viết đã được sửa đổi nội dung bởi Juliel: 10-07-2013 - 11:42
Thế này nhé ! Mình có một cách không khoa học nhưng hiệu suất cao, bạn tham khảo :
$A=sqrt[3]44+18sqrt6$
Nhận xét rằng A phải viết được dưới dạng $A=sqrt[3](a+b)^3Rightarrow A^3=(a+b)^3=a(a^2+3b^2)+b(b^2+3a^2)Rightarrow 44+18sqrt6=a(a^2+3b^2)+b(b^2+3a^2)$
Ta cứ lấy giá trị sau :
$18sqrt6=a(a^2+3b^2)Rightarrow left{beginmatrix & a=sqrt6 & \ & a^2+3b^2=18 & endmatrixright. Rightarrow $a=sqrt6;b=2$
Suy ra $A=2+sqrt6$
Với trường hợp ta làm như trên mà không tìm được a;b "đẹp" thì hoàn toàn có thể nhân 2, nhân 3 vào biểu thức A
Thi MTCT tỉnh Đồng Nai năm nay cũng luôn có thể có một câu thế này, nhờ cách này mà mình làm được đấy !
Cách của em vẫn không hiệu suất cao ... Giả sử tổng quát lên: $A=sqrt[n]a+sqrtb$ thì những cách trên không ăn được
3 bình phương bằng bao nhiêu?
Số 3 bình phương lên bằng 9.Căn A bình phương bằng bao nhiêu?
Căn thức bậc hai và hằng đẳng thức √A2=|A| (căn A bình phương bằng trị tuyệt đối của A) - Toán 9 bài 2 chương 1 tập 1. Như những em đã biết công thức tính diện tích s quy hoạnh hình vuông vắn cạnh (kích thước) a là S = a*a = a2.1 bình phương bằng bao nhiêu?
Bình phương của một số trong những là tích của số đó với chính bản thân mình nó 2 lần.3 căn 8 bằng bao nhiêu?
Vì vậy, tất cả chúng ta hoàn toàn có thể xác định căn bậc hai của 8 bằng 2, ví dụ như 3 √8 = 2. Tải thêm tài liệu liên quan đến nội dung bài viết Căn 3 bình phương bằng bao nhiêu? Hỏi Đáp Bao nhiêu
Post a Comment