Mẹo Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC
Kinh Nghiệm về Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC Mới Nhất
Bùi Thị Kim Oanh đang tìm kiếm từ khóa Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC được Update vào lúc : 2022-12-11 01:08:02 . Với phương châm chia sẻ Bí kíp về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc tài liệu vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha.Câu hỏi
Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai đoạn: BH = 4 cm và HC = 6 cm.
a) Tính độ dài những đoạn AH, AB, AC.
Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành 2 đoạn: BH=4cm, HC=6cm
a, Tính độ dài AH, AB,AC
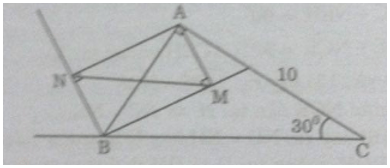
b, Gọi M là trung điểm của AC. Tính số đo góc AMB
c, Kẻ Ak vuông góc BM(K thuộc BM)
Chứng minh: tam giác BKC đồng dạng tam giác BHM
Toán Lớp 9: Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai đoạn: BH=4cm và HC = 6cm a. tính độ dài đoạn AH, AB,AC b. Gọi M là trung điểm của AC. tính số đo góc AMB (làm tròn đến độ) c. Kẻ AK vuông góc với BM (K thuộc BM) chứng tỏ BK.BM= BH.BC
ko lm tắt, hướng dẫn giải giúp em bài này ạ, em cảm ơn thầy cô và những bạn nhiều.
Giải SBT Toán 8 Bài 8: Các trường hợp đồng dạng của tam giác vuông
Bài 8.3 trang 96 sách bài tập Toán 8 Tập 2: Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9cm.
Gọi D và E là hình chiếu của H trên AB và AC.
a) Tính độ dài DE
b) Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N . Chứng minh M là trung điểm của BH , N là trung điểm của CH.
c) Tính diện tích s quy hoạnh tứ giác DENM.
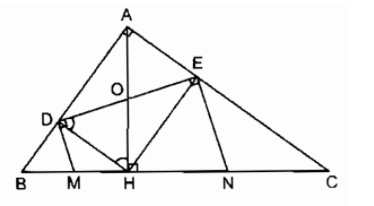
Lời giải:
a) Xét hai tam giác vuông ABH và CAH có:
ABH^=CAH^ (cùng phụ với góc BAH^)
Do đó ∆ ABH đồng dạng ∆CAH (g.g).
Suy ra: AHCH = BHAH.
⇒AH2 = BH. CH = 4.9 = 36 ⇒ AH = 6(cm)
Mặt khác, HD ⊥ AB và HE ⊥ AC nên ADHE là hình chữ nhật.
Suy ra: DE = AH = 6 (cm).
b) Vì ADHE là hình chữ nhật nên OD = OH
Suy ra, tam giác ODH cân tại O
⇒ ODH^=OHD^
Mà
ODH^ + MDH^ = 900; OHD^+ MHD^ =900⇒MDH^ = MHD^
Xét tam giác MBD có:
MDB^=MBD^ (vì cùng phụ với hai góc bằng nhau MDH^=MHD^)
Suy ra, tam giác MBD cân tại M.
Do đó MD = MB (2)
Từ (1) và (2) suy ra, MB = MH.
Vậy M là trung điểm của BH.
Tương tự, ta cũng luôn có thể có N là trung điểm của CH.
c) Theo chứng tỏ trên, ta có:
DM = MH = 12BH = 12.4 = 2(cm)
EN = NH = 12CH = 12.9 = 4,5(cm)
DE = AH = 6(cm).
DENM là hình thang vuông, do đó diện tích s quy hoạnh của nó là:
SDENM = 12(DM + EN).DE
= 12.(2 + 4,5).6 = 19,5(cm2).
Xem thêm lời giải sách bài tập Toán lớp 8 hay, rõ ràng khác:
Bài 44 trang 95 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A, AC = 9cm, BC = 24cm. Đường trung trực của BC cắt đường thẳng AC tại D, cắt BC tại M. Tính độ dài của đoạn thẳng CD...
Bài 45 trang 95 SBT Toán 8 Tập 2: Cho hình thang vuông ABCD ( A^=D^=90°); AB = 6cm, CD = 12cm, AD = 17cm. Trên cạnh AD, đặt đoạn AE = 8cm...
Bài 46 trang 95 SBT Toán 8 Tập 2: Cho tam giác ABC vuông tại A, AC = 4cm, BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A khác phía so với đường thẳng BC)...
Bài 47 trang 95 SBT Toán 8 Tập 2: Trên hình vẽ hãy chỉ ra những tam giác đồng dạng. Viết những cặp tam giác đồng dạng theo thứ tự những đỉnh tương ứng và lý giải vì sao chúng đồng dạng...
Bài 48 trang 95 SBT Toán 8 Tập 2: Cho tam giác ABC ( A^=90°) có đường cao AH. Chứng minh rằng AH2 = BH.CH...
Bài 49 trang 96 SBT Toán 8 Tập 2: Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn...
Bài 50 trang 96 SBT Toán 8 Tập 2: Tam giác vuông ABC ( A^=90°) có đường cao AH và trung tuyến AM...
Bài 8.1 trang 96 SBT Toán 8 Tập 2: Cho góc nhọn xOy. Trên tia Ox lấy một điểm A sao cho OA = 8,65cm...
Bài 8.2 trang 96 SBT Toán 8 Tập 2: Tam giác ABC vuông tại A có đường cao AH = n = 10,85cm và cạnh AB = m = 12,5cm...
a) $AH^2=BH.HC⇒AH=sqrt4.6=sqrt24⇒AH=2sqrt6$ (cm)
$AB=sqrtAH^2+BH^2=sqrt(2sqrt6)^2+4^2=2sqrt10$ (cm)
$AC=sqrtAH^2+HC^2=sqrt(2sqrt6)^2+6^2=2sqrt15$ (cm)
b) $AM=dfrac12AC=dfrac2sqrt152=sqrt15$
Áp dụng hệ thức lượng giác vào $Delta ABM$ có:
$tan widehatAMB=dfracABAM=dfrac2sqrt10sqrt15 Rightarrow widehatAMB=58,518^o≈59^o$
c) Áp dụng định lý Pitago ta có: $BM=sqrtAB^2+AM^2=sqrt55$
$AB^2=BK.BM⇒BK=dfracAB^2BM=dfrac40sqrt55$
Ta có: $widehat KBC=widehatHBM$ đều là một góc
$dfracBKBH=dfrac40sqrt55.4=dfrac10sqrt55$
Mà $dfracBCBM=dfrac10sqrt55⇒dfracBKBH=dfracBCBM=dfrac10sqrt55$
$Rightarrow ΔBKCsim Δ BHM$ (c.g.c)


Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH. Câu 96 trang 112 Sách Bài Tập (SBT) Toán 9 Tập 1 – Ôn tập chương I
Advertisements (Quảng cáo)
Cho tam giác ABC vuông tại A, đường cao AH chia cạnh huyền BC thành hai đoạn BH, CH có độ dài lần lượt là 4cm, 9cm. Gọi D và E lần lượt là hình chiếu của H trên AB và AC.
a) Tính độ dài đoạn thẳng DE.
b) Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH.
c) Tính diện tích s quy hoạnh tứ giác DENM.
Gợi ý làm bài
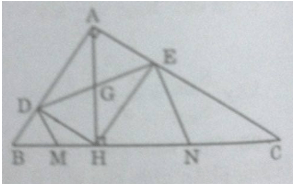
a) Ta có:
(HD bot AB Rightarrow widehat ADH = 90^circ )
(HE bot AC Rightarrow widehat AEH = 90^circ )
Tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật.
Suy ra: AH = DE (tính chất hình chữ nhật)
Tam giác ABC vuông tại A và có AH là đường cao.
Theo hệ thức liên hệ giữa đường cao và hình chiếu ta có:
(eqalign & AH^2 = HB.HC = 4.9 = 36 cr
& Rightarrow AH = 6,(cm) cr )
Vậy DE = 6 (cm)
b) * Gọi G là giao điểm của AH và DE
Ta có: GA = GD = GH = GE (tính chất hình chữ nhật)
Suy ra tam giác GHD cân tại G
Ta có:
(widehat GDH = widehat GHD,(1))
(widehat GDH + widehat MDH = 90^circ ,(2))
(widehat GHD + widehat MHD = 90^circ ,(3))
Từ (1), (2) và (3) suy ra: (widehat MDH = widehat MHD,(4))
Suy ra tam giác MDH cân tại M ( Rightarrow MD = MH,(5))
Lại có: (widehat MDH + widehat MDB = 90^circ ,(6))
Advertisements (Quảng cáo)
(widehat MBD + widehat MHD = 90^circ ) (∆BDH vuong tại D) (7)
Từ (4), (6) và (7) suy ra: (widehat MDB = widehat MBD)
Suy ra tam giác MBD cân tại M ( Rightarrow MB = MD,(8))
Từ (5) và (8) suy ra: MB = MH hay M là trung điểm của BH.
*Tam giác GHE cân tại G
Ta có: (widehat GHE = widehat GEH,(9))
(widehat GHE + widehat NHE = 90^circ ) (10)
(widehat GEH + widehat NEH = 90^circ ) (11)
Advertisements (Quảng cáo)
Từ (9), (10) và (11) suy ra: (widehat NHE = widehat NEH) (12)
Suy ra tam giác NEH cân tại n ( Rightarrow NE = NH) (13)
Lại có: (widehat NEC + widehat NEH = 90^circ ) (14)
(widehat NHE + widehat NCE = 90^circ ) (∆CEH vuông tại E) (15)
Từ (12), (14) và (15) suy ra: (widehat NDC = widehat NCE)
Suy ra tam giác NCE cân tại N ( Rightarrow NC = NE,(16))
Từ (13) và (16) suy ra: NC = NH hay N là trung điểm của CH.
c) Tam giác BDH vuông tại D có DM là đường trung tuyến nên:
(DM = 1 over 2BH = 1 over 2.4 = 2,(cm))
Tam giác CEH vuông tại E có EN là đường trung tuyến nên
(EN = 1 over 2CH = 1 over 2.9 = 4,5,(cm))
Mà (MD bot DE) và NE bot DE) nên MD // NE
Suy ra tứ giác DENM là hình thang
Vậy
(eqalign & S_DENM = DM + NE over 2.DE cr
& = 2 + 4,5 over 2.6 = 19,5 cr ) (cm2).
Tải thêm tài liệu liên quan đến nội dung bài viết Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC
Post a Comment