Home
bài
Giải

Review Giải bài tập SGK Toán 9 tập 1 trang 59

Kinh Nghiệm Hướng dẫn Giải bài tập SGK Toán 9 tập 1 trang 59 Mới Nhất

Hoàng T Thu Thủy đang tìm kiếm từ khóa Giải bài tập SGK Toán 9 tập 1 trang 59 được Update vào lúc : 2022-11-10 02:46:02 . Với phương châm chia sẻ Bí kíp về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Admin lý giải và hướng dẫn lại nha.

Nội dung chính Show
    Lý thuyết1. Khái niệm thông số góc của đường thẳng $y = ax + b (a ≠ 0)$.2. Tính chấtLuyện tập1. Giải bài 29 trang 59 sgk Toán 9 tập 12. Giải bài 30 trang 59 sgk Toán 9 tập 13. Giải bài 31 trang 59 sgk Toán 9 tập 1Video liên quan

    Chương 1: Căn bậc hai. Căn bậc ba

    Chương 2: Hàm số số 1

    Giải Toán 9 tập 1 Hình học

    Chương 1: Hệ thức lượng trong tam giác vuông

    Chương 3: Hệ hai phương trình số 1 hai ẩn

    Chương 4: Hàm số y=ax^2 (a ≠0). Phương trình bậc hai một ẩn

    Giải Toán 9 tập 2 Hình học

    Chương 3: Góc với đường tròn

    Chương 4: Hình trụ - Hình nón – Hình cầu

Luyện tập Bài §5. Hệ số góc của đường thẳng (y = ax + b (a ≠ 0)), chương II – Hàm số số 1, sách giáo khoa toán 9 tập một. Nội dung bài giải bài 29 30 31 trang 59 sgk toán 9 tập 1 gồm có tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần đại số có trong SGK toán để giúp những em học viên học tốt môn toán lớp 9.

Lý thuyết

1. Khái niệm thông số góc của đường thẳng $y = ax + b (a ≠ 0)$.

Xét đường thẳng (y=ax+b (a neq 0)). Khi đó a được gọi là thông số góc của đường thẳng (y=ax+b)

2. Tính chất

Gọi A là giao điểm của đường thẳng (y=ax+b) và trục Ox, T là vấn đề thuộc đường thẳng (y=ax+b) và có tung độ dương. Ta gọi góc tạo bởi đường thẳng (y=ax+b) và trục Ox là góc tạo bởi tia AT và tia Ax. Đặt góc đó là (alpha)

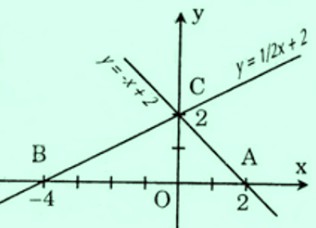
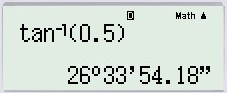
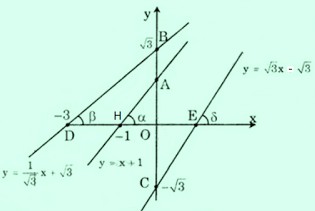
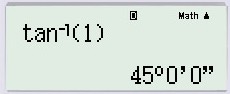
Nếu (a>0) thì (0^circ

Nếu (a<0) thì (0^circ

Dưới đây là Hướng dẫn  giải bài 29 30 31 trang 59 sgk toán 9 tập 1. Các bạn hãy tham khảo kỹ đầu bài trước khi giải nhé!

Luyện tập

Giaibaisgk.com ra mắt với những bạn đầy đủ phương pháp giải bài tập phần đại số 9 kèm bài giải rõ ràng bài 29 30 31 trang 59 sgk toán 9 tập 1 của bài §5. Hệ số góc của đường thẳng (y = ax + b (a ≠ 0)) trong chương II – Hàm số số 1 cho những bạn tham khảo. Nội dung rõ ràng bài giải từng bài tập những bạn xem dưới đây:

Giải bài tập SGK Toán 9 tập 1 trang 59Giải bài 29 30 31 trang 59 sgk toán 9 tập 1

1. Giải bài 29 trang 59 sgk Toán 9 tập 1

Xác định hàm số số 1 $y = ax + b$ trong mỗi trường hợp sau:

a) $a = 2$ và đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng $1,5$.

b) $a = 3$ và đồ thị của hàm số đi qua điểm $A(2; 2)$.

c) Đồ thị của hàm số song song với đường thẳng $y = sqrt3x$ và đi qua điểm $B(1; sqrt3 + 5)$.

Bài giải:

Hàm số đã cho là (y = ax + b). ((1))

a) Theo giả thiết (a=2 Rightarrow y=2x+b.) ((2))

Vì đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng (1,5)

Suy ra tung độ bằng (0). Thay (x=1,5, y=0) vào ((2)), ta được:

(0=2.1,5+b Leftrightarrow 0=3+b)

( Leftrightarrow b=-3)

Vậy hàm số đã cho là (y = 2x – 3.)

b) Theo giả thiết (a=3 Rightarrow y=3x+b) ((3))

Vì đồ thị đi qua điểm (A(2; 2)) nên tọa độ của (A) là nghiệm của phương trình ((3)). Thay (x=2, y=2) vào ((3)), ta được:

(2=3.2+b Leftrightarrow 2=6+b)

(Leftrightarrow 2-6=b) (Leftrightarrow b=-4)

Vậy hàm số đã cho là (y = 3x – 4.)

c) Vì đồ thị hàm số đã cho song song với đường thẳng (y=sqrt 3 x) nên (a=sqrt 3). Do đó hàm số đã cho là (y = sqrt 3 x + b) ((4))

Thay (x=1, y=sqrt 3 + 5) vào ((4)), ta được:

(sqrt 3 + 5 = sqrt 3 .1 + b Leftrightarrow sqrt 3 + 5- sqrt 3=b).

(Leftrightarrow (sqrt 3 – sqrt 3) + 5=b).

(Leftrightarrow b=5 ™)

Vậy hàm số đã cho là (y = sqrt 3 x + 5)

2. Giải bài 30 trang 59 sgk Toán 9 tập 1

a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của những hàm số sau:

$y = frac12x + 2 ;  y = -x + 2$

b) Gọi giao điểm của hai tuyến đường thẳng $y = frac12x + 2$ và $y = -x + 2$ với trục hoành theo thứ tự là $A, B$ và gọi giao điểm của hai tuyến đường thẳng đó là $C$. Tính những góc của tam giác $ABC$ (làm tròn đến độ).

c) Tính chu vi và diện tích s quy hoạnh của tam giác $ABC$ (đơn vị đo trên những trục tọa độ là xentimet).

Bài giải:

a) Vẽ đồ thị hàm số $y = frac12x + 2$

– Cho $x = 0 ⇒ y = 2$, ta xác định được điểm $C(0; 2)$

– $Cho y = 0 ⇒ x = -4$, ta xác định được điểm $B(-4; 0)$

Đồ thị hàm số $y = frac12x + 2$ là đường thẳng đi qua hai điểm $C(0; 2)$ và $B(-4; 0)$.

Vẽ đồ thị hàm số $y = -x + 2$

– Cho $x = 0 ⇒ y = 2$, ta xác định được điểm $C(0; 2)$

– Cho $y = 0 ⇒ x = 2$, ta xác định được điểm $A(2; 0)$

Đồ thị hàm số $y = -x + 2$ là đường thẳng đi qua hai điểm $C(0; 2)$ và $A(2; 0)$

Giải bài tập SGK Toán 9 tập 1 trang 59

b) – Xét tam giác $OBC$, ta có:

$tgwidehatCBO$ = $fracOCOB$ = $frac24$ = $frac12$

Do đó $widehatCBA$ = $widehatCBO$ = $26^0$33′ $approx$ $26^0$

Thực hiện bấm máy tính, ta được:

Giải bài tập SGK Toán 9 tập 1 trang 59

– Xét tam giác $OAC$, ta có:

$tg widehatCAO$ = $fracOCOA$ = $frac22$ = 1

Do đó $widehatCAO$ = $widehatCAB$ = $45^0$

– Xét (DeltaABC) có: (widehatA+ widehatB+widehatC=180^o)

(Leftrightarrow widehatC=180^o-widehatA-widehatB)

(Leftrightarrow widehatC approx 180^o-26^o-45^o)

(Leftrightarrow widehatC approx 109^o)

c) Ta có: (AB = 6 (cm))

Xét tam giác vuông (OBC) vuông tại (O), theo định lí Py-ta-go, ta có:

(BC^2=BO^2+OC^2=4^2+2^2=16+4=20)

(Rightarrow BC =sqrt20=2sqrt5(cm))

Xét tam giác vuông (OAC) vuông tại (O), ta có:

(AC^2=AO^2+OC^2=2^2+2^2=4+4=8)

(Rightarrow AC =sqrt 8 = 2sqrt2(cm))

(DeltaOAC) có (OC bot AB) nên (OC) là đường cao ứng với cạnh (AB).

Chu vi tam giác là:

(P=AB+BC+AC=6+2sqrt5+2sqrt2 (cm))

Diện tích tam giác là:

(S=dfrac12.OC.AB=dfrac12.2.6=6 (cm^2))

3. Giải bài 31 trang 59 sgk Toán 9 tập 1

a) Vẽ đồ thị của những hàm số $y = x + 1$; y = $frac1sqrt3$ + $sqrt3$; y = $sqrt3$x – $sqrt3$

b) Gọi $alpha$, $beta$, $gamma$ lần lượt là những góc tạo bởi những đường thẳng trên và trục Ox. Chứng minh rằng tg$alpha$ = 1; tg$beta$ = $frac1sqrt3$; tg$gamma$ = $sqrt3$

Tính số đo những góc $alpha$, $beta$, $gamma$.

Bài giải:

a) Vẽ đồ thị của những hàm số

+ (y = x + 1)

Cho (x=0 Rightarrow y=0+1=1 Rightarrow A(0; 1))

Cho (x=-1 Rightarrow y=-1+1=0 Rightarrow H(-1; 0))

Đồ thị hàm số (y = x + 1) là đường thẳng đi qua hai điểm (A(0; 1)) và (H(-1; 0))

+ (y = dfrac1sqrt 3 x + sqrt 3)

Cho (x=-3 Rightarrow y = dfrac1sqrt 3 .(-3) + sqrt 3=0 Rightarrow D(-3; 0))

Cho (x=0 Rightarrow y = dfrac1sqrt 3 .0 + sqrt 3 =sqrt 3 Rightarrow B(0; sqrt 3))

Đồ thị hàm (y = dfrac1sqrt 3 x + sqrt 3) là đường thẳng đi qua hai điểm (D(-3; 0)) và (B(0; sqrt 3))

+ (y = sqrt 3 x – sqrt 3)

Cho (x=0 Rightarrow y = sqrt 3 .0 – sqrt 3=sqrt 3 Rightarrow C(0; sqrt 3))

Cho (x=1 Rightarrow y = sqrt 3 .1 – sqrt 3=0 Rightarrow E(1; 0))

Đồ thị hàm số (y = sqrt 3 x – sqrt 3) là đường thẳng đi qua hai điểm (C(0; sqrt 3)) và (E(1; 0))

Giải bài tập SGK Toán 9 tập 1 trang 59

b) ♦ Cách 1:

+ Đường thẳng (y = x + 1) có thông số góc là (1)

Suy ra (tan alpha = 1 Leftrightarrow alpha = 45^o)

+ Đường thẳng (y = dfrac1sqrt 3 x + sqrt 3) có thông số góc là (dfrac1sqrt 3 )

Suy ra (tan beta = dfrac1sqrt 3 Leftrightarrow beta = 30^o)

+ Đường thẳng (y = sqrt 3 x – sqrt 3) có thông số góc là (sqrt 3)

Suy ra (tan gamma = sqrt 3 Leftrightarrow alpha = 60^o)

♦ Cách 2:

+ Quan sát hình vẽ, hay thấy:

(OA=OH=OE=1), (OB=OC=sqrt 3), (OD = 3).

+ Xét (DeltaOAH) vuông tại (O)

(Rightarrow tan alpha =tan H =dfracOAOB=dfrac11=1)

(Rightarrow alpha = 45^o)

Thực hiện bấm máy tính:

Giải bài tập SGK Toán 9 tập 1 trang 59

+ Xét (DeltaODB) vuông tại (O)

(Rightarrow tan beta =tan D =dfracOBOD=dfracsqrt 33)

(Rightarrow beta = 30^o)

+ Xét (DeltaOEC) vuông tại (O)

(Rightarrow tan beta =tan widehatOFE =dfracOEOC=dfracsqrt 31=sqrt 3)

(Rightarrow gamma = 60^o)

Lại có (widehatOEC) và (gamma) là hai góc đối đỉnh (Rightarrow widehatOEC=gamma).

Vậy (gamma=60^o).

Bài trước:

    Giải bài 27 28 trang 58 sgk Toán 9 tập 1

Bài tiếp theo:

    Trả lời thắc mắc 1 2 trang 59 60 sgk Toán 9 tập 1

Xem thêm:

Chúc những bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 29 30 31 trang 59 sgk toán 9 tập 1!

“Bài tập nào khó đã có giaibaisgk.com“

Tải thêm tài liệu liên quan đến nội dung bài viết Giải bài tập SGK Toán 9 tập 1 trang 59 Khỏe Đẹp Bài tập

Clip Giải bài tập SGK Toán 9 tập 1 trang 59 ?

Bạn vừa đọc nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Video Giải bài tập SGK Toán 9 tập 1 trang 59 tiên tiến nhất

Chia Sẻ Link Cập nhật Giải bài tập SGK Toán 9 tập 1 trang 59 miễn phí

Bạn đang tìm một số trong những Chia SẻLink Download Giải bài tập SGK Toán 9 tập 1 trang 59 Free.

Hỏi đáp thắc mắc về Giải bài tập SGK Toán 9 tập 1 trang 59

Nếu sau khi đọc nội dung bài viết Giải bài tập SGK Toán 9 tập 1 trang 59 vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Admin lý giải và hướng dẫn lại nha #Giải #bài #tập #SGK #Toán #tập #trang

Post a Comment