Mẹo Bài 7 trang 26 SGK Toán Hình 10
Thủ Thuật về Bài 7 trang 26 SGK Toán Hình 10 Chi Tiết
Lê Nguyễn Hà Linh đang tìm kiếm từ khóa Bài 7 trang 26 SGK Toán Hình 10 được Cập Nhật vào lúc : 2022-11-23 05:28:04 . Với phương châm chia sẻ Bí quyết về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi tham khảo tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
Đề bài
Các điểm (A'(-4; 1), B'(2;4), C'(2, -2)) lần lượt là trung điểm của những cạnh (BC, CA) và (AB) của tam giác (ABC). Tính tọa độ đỉnh của tam giác (ABC). Chứng minh rằng trọng tâm tam giác (ABC) và (A'B'C') trùng nhau.
Video hướng dẫn giải
[embed]https://www.youtube.com/watch?v=hKp6l8-QA78[/embed]Phương pháp giải - Xem rõ ràng
+) (I) là trung điểm của (AB) thì: (left{ beginarrayl
x_I = fracx_A + x_B2\
y_I = fracy_A + y_B2
endarray right..)
+) (G) là trọng tâm tam giác (ABC) thì: (left{ beginarraylx_G = fracx_A + x_B + x_C3\y_G = fracy_A + y_B + y_C3endarray right..)
Lời giải chi tiết
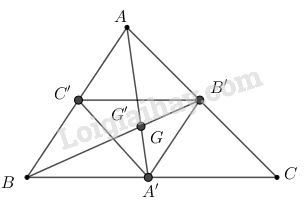
Giả sử (A(x_A;y_A),B(x_B;y_B),C(x_C;y_C))
(A') là trung điểm BC ( Leftrightarrow left{ beginarraylx_A' = fracx_B + x_C2\y_A' = fracy_B + y_C2endarray right.)
( Leftrightarrow left{ beginarrayl - 4 = fracx_B + x_C2\1 = fracy_B + y_C2endarray right.) ( Leftrightarrow left{ beginarraylx_B + x_C = - 8,left( 1 right)\y_B + y_C = 2,left( 2 right)endarray right.)
(B') là trung điểm CA ( Leftrightarrow left{ beginarraylx_B' = fracx_C + x_A2\y_B' = fracy_C + y_A2endarray right.)
( Leftrightarrow left{ beginarrayl2 = fracx_C + x_A2\4 = fracy_C + y_A2endarray right.) ( Leftrightarrow left{ beginarraylx_C + x_A = 4,left( 3 right)\y_C + y_A = 8,left( 4 right)endarray right.)
(C') là trung điểm AB ( Leftrightarrow left{ beginarraylx_C' = fracx_A + x_B2\y_C' = fracy_A + y_B2endarray right.)
( Leftrightarrow left{ beginarrayl2 = fracx_A + x_B2\ - 2 = fracy_A + y_B2endarray right.) ( Leftrightarrow left{ beginarraylx_A + x_B = 4,left( 5 right)\y_A + y_B = - 4,left( 6 right)endarray right.)
Từ (1), (3) và (5) ta có hệ:
(left{ beginarraylx_B + x_C = - 8\x_C + x_A = 4\x_A + x_B = 4endarray right. Leftrightarrow left{ beginarraylx_C = - 8 - x_B\ - 8 - x_B + x_A = 4\x_A + x_B = 4endarray right.) ( Leftrightarrow left{ beginarraylx_C = - 8 - x_B\x_A - x_B = 12\x_A + x_B = 4endarray right. Leftrightarrow left{ beginarraylx_A = 8\x_B = - 4\x_C = - 4endarray right.)
Từ (2), (4) và (6) ta có hệ:
(left{ beginarrayly_B + y_C = 2\y_C + y_A = 8\y_A + y_B = - 4endarray right. Leftrightarrow left{ beginarrayly_C = 2 - y_B\2 - y_B + y_A = 8\y_A + y_B = - 4endarray right.) ( Leftrightarrow left{ beginarrayly_C = 2 - y_B\y_A - y_B = 6\y_A + y_B = - 4endarray right. Leftrightarrow left{ beginarrayly_A = 1\y_B = - 5\y_C = 7endarray right.)
Vậy (Aleft( 8;1 right),Bleft( - 4; - 5 right),Cleft( - 4;7 right)).
Gọi (G(x_G;y_G)) là trọng tâm của tam giác (ABC)
Khi đó ta có:
(left{ matrix
x_G = x_A + x_B + x_C over 3 = 8 - 4 - 4 over 3 = 0 hfill cr
y_G = y_A + y_B + y_C over 3 = 1 - 5 + 7 over 3 = 1 hfill cr right.)
Vậy (G(0;1)) (*)
Gọi (G'(x_G';y_G')) là trọng tâm của tam giác (A'B'C')
Khi đó ta có:
(left{ matrix
x_G' = x_A' + x_B' + x_C' over 3 = - 4 + 2 + 2 over 3 = 0 hfill cr
y_G' = y_A' + y_B' + y_C' over 3 = 1 + 4 - 2 over 3 = 1 hfill cr right.)
Vậy (G'(0;1)) (**)
Từ (*) và (**) ta thấy (G equiv G')
Vậy trọng tâm tam giác (ABC) và (A'B'C') trùng nhau.
Loigiaihay.com
- Bài 8 trang 27 SGK Hình học 10
Giải bài 8 trang 27 SGK Hình học 10. Hãy phân tích vectơ
Bài 6 trang 27 (Hệ trục tọa độ) SGK Hình học 10Cho hình bình hành ABCD có A(-1; -2), B(3;2), C(4;-1). Tìm tọa độ điểm D.
Bài 5 trang 27 (Hệ trục tọa độ) SGK Hình học 10Giải Bài 5 trang 27 (Hệ trục tọa độ) SGK Hình học 10. Trong những mặt phẳng Oxy cho điểm...
Bài 4 trang 26 SGK Hình học 10Trong mặt phẳng Oxy. Các xác định sau đúng hay sai?
Bài 3 trang 26 SGK Hình học 10Giải bài 3 trang 26 SGK Hình học 10. Tìm tọa độ của những vec tơ sau:
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Báo lỗi - Góp ý
>> Học trực tuyến Lớp 10 tại Tuyensinh247.com, Cam kết giúp học viên học tốt, hoàn trả học phí nếu học không hiệu suất cao.
Tải thêm tài liệu liên quan đến nội dung bài viết Bài 7 trang 26 SGK Toán Hình 10
Post a Comment