Review What do you call the measure of central tendency that points the middle value in an array of observations?
Thủ Thuật về What do you call the measure of central tendency that points the middle value in an array of observations? Chi Tiết
Bùi Công Duy đang tìm kiếm từ khóa What do you call the measure of central tendency that points the middle value in an array of observations? được Update vào lúc : 2022-10-18 00:14:05 . Với phương châm chia sẻ Kinh Nghiệm về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha.A descriptive summary of a dataset through a single value that reflects the center of the data distribution
Nội dung chính- What is Central Tendency?Measures of Central TendencyRelated ReadingsBasic ConceptsWorksheet FunctionsHandling non-numeric dataWhat measure of central tendency where it is the middle value of the observation?What do you call the measure of central tendency that points to the value that occurs most often or the value with the highest frequency in a set of data?What do you call the measure of central tendency that is referred to as the most frequently occurring value in a given set?What do you call the measure of central tendency which is the sum of the values of the data divided by the total number of values?
What is Central Tendency?
Central tendency is a descriptive summary of a dataset through a single value that reflects the center of the data distribution. Along with the variability (dispersion) of a dataset, central tendency is a branch of descriptive statistics.
The central tendency is one of the most quintessential concepts in statistics. Although it does not provide information regarding the individual values in the dataset, it delivers a comprehensive summary of the whole dataset.
Measures of Central Tendency
Generally, the central tendency of a dataset can be described using the following measures:
- Mean (Average): Represents the sum of all values in a
dataset divided by the total number of the values.Median: The middle value in a dataset that is arranged in ascending order (from the smallest value to the largest value). If a dataset contains an even number of values, the median of the dataset is the mean of the two middle values.Mode: Defines the most frequently occurring value in a dataset. In some cases, a dataset may contain multiple modes, while some datasets may not have any mode
all.
Even though the measures above are the most commonly used to define central tendency, there are some other measures, including, but not limited to, geometric mean, harmonic mean, midrange, and geometric median.
The selection of a central tendency measure depends on the properties of a dataset. For instance, the mode is the only central tendency measure for categorical data, while a median works best with ordinal data.
Although the mean is regarded as the best measure of central tendency for quantitative data, that is not always the case. For example, the mean may not work well with quantitative datasets that contain extremely large or extremely small values. The extreme values may distort the mean. Thus, you may consider other measures.
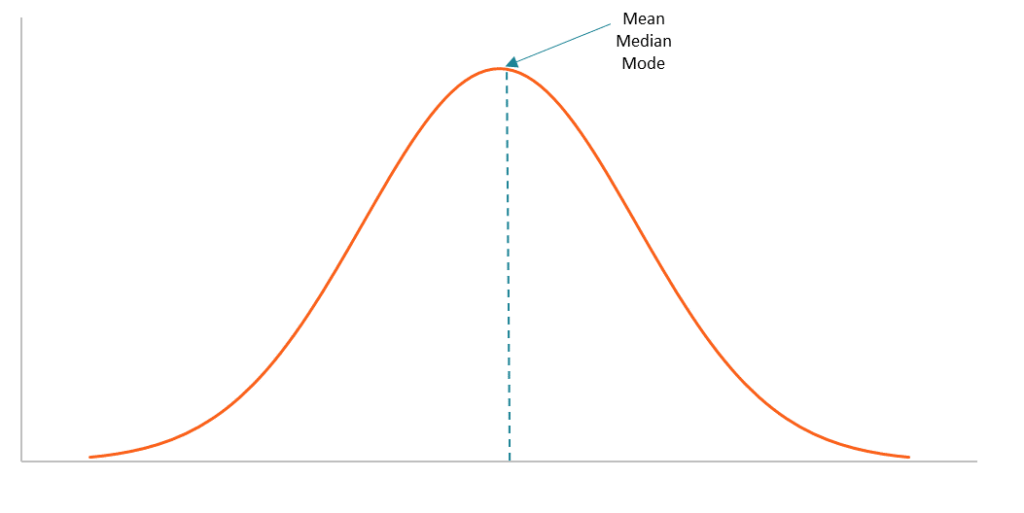
The measures of central tendency can be found using a formula or definition. Also, they can be identified using a frequency distribution graph. Note that for datasets that follow a normal distribution, the mean, median, and mode are located on the same spot on the graph.
Related Readings
Thank you for reading CFI’s guide on Central Tendency. To keep learning and advancing your career, the following resources will be helpful:
- Free Statistics Fundamentals CourseComprehensive List of Excel FunctionsDynamic Dates, Sum, Average,
and ScenariosQuantitative AnalysisStandard Deviation
Basic Concepts
We consider a random variable x and a data set S = x1, x2, …, xn of size n which contains values for x. The data in S can represent either a population being studied or a sample drawn from such a population. We can also view the data as defining a distribution, as described in Discrete Probability Distributions.
We seek a single measure (i.e. a statistic) that somehow represents the center of the entire data set S. The commonly used measures of central tendency are the mean, median, and mode. Besides the normally studied mean (also called the arithmetic mean), we also consider two other types of mean: the geometric mean and the harmonic mean.
Worksheet Functions
Excel Functions: If R1 is an array or range that contains the data elements in S then the Excel formula that calculates each of these statistics is shown in Figure 1.

Figure 1 – Measures of central tendency
Handling non-numeric data
While formulas such as AVERAGE(R1) (as well as VAR(R1), STDEV(R1), etc. described on other webpages) ignore any empty or non-numeric cells, they return an error value if R1 contains an error value such as #NUM or #DIV/0!. This limitation can often be overcome by using one of the following array formulas:
=AVERAGE(IF(ISERROR(R1), ””, R1))
=AVERAGE(IFERROR(R1, ””)
These formulas return the mean of all the cells in R1 ignoring any cells that contain an error value. Since these are array formulas, you must press Ctrl-Shft-Enter (unless you are using Excel 365). An alternative approach is to use the Real Statistics DELErr function.
Worksheet FunctionReal Statistics Function: The Real Statistics Resource Pack provides the following array function:
DELErr(R1) = the array of the same size and shape as R1 consisting of all the elements in R1 where any cells with an error value are replaced by a blank (i.e. an empty cell).
E.g. to find the average of the elements in an array R1 which may contain error values, you can use the formula
=AVERAGE(DELErr(R1))
In this case, you only need to press the Enter key and don’t have to press Ctrl-Shft-Enter.
Data Analysis ToolReal Statistics Data Analysis Tool: The Remove error cells option of the Reformatting a Data Range data analysis tool described in Reformatting Tools makes a copy of the inputted range where all cells that contain error values are replaced by empty cells.
To use this capability, press Ctrl-m and double click on Reformatting a Data Range. When the dialog box shown in Figure 2 of Reformatting Tools, fill in the Input Range, choose the Remove error cells option and leave the # of Rows and # of Columns fields blank. The output will have the same size and shape as the input range.
Mean
We begin with the most commonly used measure of central tendency, the mean.
Definition 1: The mean (also called the arithmetic mean) of the data set S is defined by
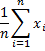
Excel Function: The mean is calculated in Excel using the function AVERAGE.
Example 1: The mean of S = 5, 2, -1, 3, 7, 5, 0, 2 is (2 + 5 – 1 + 3 + 7 + 5 + 0 + 2) / 8 = 2.875. We achieve the same result by using the formula =AVERAGE(C3:C10) in Figure 2.

Figure 2 – Excel examples of central tendency
Observation: When the data set S is a population the Greek letter µ is used for the mean. When S is a sample, then the symbol x̄ is used.
Observation: When data is expressed in the form of frequency tables then the following property is useful.
Property 1: If x̄ is the mean of sample x1, x2, …, xm and ȳ is the mean of sample y1, y2, …, yn then the mean of the combined sample is
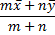
Similarly, if µx is the mean of population x1, x2, …, xm and µy is the mean of population y1, y2, …, yn then the mean of the combined population is
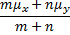
Real Statistics Functions: The Real Statistics Resource Pack furnishes the following array functions:
COUNTCOL(R1) = a row range that contains the number of numeric elements in each of the columns in R1
SUMCOL(R1) = a row range that contains the sums of each of the columns in R1
MEANCOL(R1) = a row range that contains the means of each of the columns in R1
COUNTROW(R1) = a column range that contains the number of numeric elements in each of the rows in R1
SUMROW(R1) = a column range that contains the sums of each of the rows in R1
MEANROW(R1) = a column range that contains the means of each of the rows in R1
Example 2: Use the COUNTCOL and MEANCOL functions to calculate the number of cells in each of the three columns in the range L4:N11 of Figure 3 as well as their means.
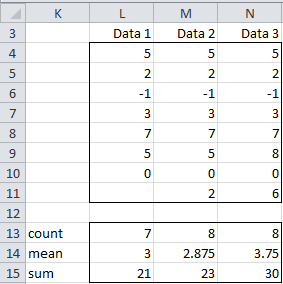
Figure 3 – Count, Sum and Mean by Column
The array formula =COUNTCOL(L4:N11) produces the first result (in range L13:N13), while the formula =MEANCOL(L4:N11) produces the second result (in range L14:N14) and the formula =SUMCOL(L4:N11) produces the third result (in range L15:N15).
Remember that after entering any of these formulas you must press Ctrl-Shft-Enter.
See Weighted Mean and Median for how to calculate the weighted mean.
Median
Definition 2: The median of the data set S is the middle value in S. If you arrange the data in increasing order the middle value is the median. When S has an even number of elements there are two such values; the average of these two values is the median.
Excel Function: The median is calculated in Excel using the function MEDIAN.
Example 3: The median of S = 5, 2, -1, 3, 7, 5, 0 is 3 since 3 is the middle value (i.e the 4th of 7 values) in -1, 0, 2, 3, 5, 5, 7. We achieve the same result by using the formula =MEDIAN(B3:B10) in Figure 2.
Note that each of the functions in Figure 2 ignores any non-numeric values, including blanks. Thus the value obtained for =MEDIAN(B3:B10) is the same as that for =MEDIAN(B3:B9).
The median of S = 5, 2, -1, 3, 7, 5, 0, 2 is 2.5 since 2.5 is the average of the two middle value 2 and 3 of -1, 0, 2, 2, 3, 5, 5, 7. This is the same result as =MEDIAN(C3:C10) in Figure 2.
See Weighted Mean and Median for how to calculate the weighted median.
Mode
Definition 3: The mode of the data set S is the value of the data element that occurs most often.
Example 4: The mode of S = 5, 2, -1, 3, 7, 5, 0 is 5 since 5 occurs twice, more than any other data element. This is the result we obtain from the formula =MODE(B3:B10) in Figure 2. When there is only one mode, as in this example, we say that S is unimodal.
If S = 5, 2, -1, 3, 7, 5, 0, 2, the mode of S consists of both 2 and 5 since they each occur twice, more than any other data element. When there are two modes, as in this case, we say that S is bimodal.
Excel Function: The mode is calculated in Excel by the formula MODE. If range R contains unimodal data then MODE(R) returns this unique mode. For the first data set in Example 3, this is 5. When R contains data with more than one mode, MODE(R) returns the first of these modes. For the second data set in Example 4, this is 5 (since 5 occurs before 2, the other mode, in the data set). Thus MODE(C3:C10) = 5.
As remarked above, if there is more than one mode, MODE returns only the first, although if all the values occur only once then MODE returns an error value. This is the case for S = 5, 2, -1, 3, 7, 4, 0, 6. Thus MODE(D3:D10) = #N/A.
Starting with Excel 2010 the array function MODE.MULT is provided which is useful for multimodal data by returning a vertical list of modes. When we highlight C19:C20 and enter the array formula =MODE.MULT(C3: C10) and then press Ctrl-Alt-Enter, we see that both modes are displayed.
The function MODE.SNGL is also provided with versions of Excel starting with Excel 2010. This function is equivalent to MODE.
Geometric Mean
Definition 4: The geometric mean of the data set S is calculated by
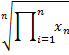
This statistic is commonly used to provide a measure of the average rate of growth as described in Example 5.
Example 5: Suppose the sales of a certain product grow 5% in the first two years and 10% in the next two years, what is the average rate of growth over the 4 years?
If sales in year 1 are $1 then sales the end of the 4 years are (1 + .05)(1 + .05)(1 + .1)(1 + .1) = 1.334. The annual growth rate r is that amount such that (1+r)4 = 1.334. Thus r = 1.3341/4 – 1 = .0747.
The same annual growth rate of 7.47% can be obtained in Excel using the formula GEOMEAN(H7:H10) – 1 = .0747.
Harmonic Mean
Definition 5: The harmonic mean of the data set S is calculated by the formula
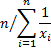
The harmonic mean can be used to calculate an average speed, as described in Example 6.
Example 6: If you go to your destination 50 mph and return 70 mph, what is your average rate of speed?
Assuming the distance to your destination is d, the time it takes to reach your destination is d/50 hours and the time it takes to return is d/70, for a total of d/50 + d/70 hours. Since the distance for the whole trip is 2d, your average speed for the whole trip is
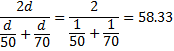
This is equivalent to the harmonic mean of 50 and 70, and so can be calculated in Excel as HARMEAN(50,70), which is HARMEAN(G7:G8) from Figure 2.
References
Wikipedia (2012)
Mean
https://en.wikipedia.org/wiki/Mean
Microsoft (2022) HARMEAN function
https://support.microsoft.com/en-us/office/harmean-function-5efd9184-fab5-42f9-b1d3-57883a1d3bc6
What measure of central tendency where it is the middle value of the observation?
The median is the middle value in distribution when the values are arranged in ascending or descending order. The median divides the distribution in half (there are 50% of observations on either side of the median value). In a distribution with an odd number of observations, the median value is the middle value.What do you call the measure of central tendency that points to the value that occurs most often or the value with the highest frequency in a set of data?
Measures of central tendency help you find the middle, or the average, of a data set. The 3 most common measures of central tendency are the mean, median and mode. The mode is the most frequent value. The median is the middle number in an ordered data set.What do you call the measure of central tendency that is referred to as the most frequently occurring value in a given set?
Mean (Arithmetic) The mean (or average) is the most popular and well known measure of central tendency. It can be used with both discrete and continuous data, although its use is most often with continuous data (see our Types of Variable guide for data types).What do you call the measure of central tendency which is the sum of the values of the data divided by the total number of values?
The mean, often called the average, of a numerical set of data, is simply the sum of the data values divided by the number of values. This is also referred to as the arithmetic mean. The mean is the balance point of a distribution. Tải thêm tài liệu liên quan đến nội dung bài viết What do you call the measure of central tendency that points the middle value in an array of observations? Measures of variability Measure of dispersion Mean in statistics
Post a Comment