Review Find the least number which when divided by 12,16,24 and 36 leaves a remainder 7 in each case
Thủ Thuật về Find the least number which when divided by 12,16,24 and 36 leaves a remainder 7 in each case 2022
Bùi An Phú đang tìm kiếm từ khóa Find the least number which when divided by 12,16,24 and 36 leaves a remainder 7 in each case được Update vào lúc : 2022-10-05 04:26:10 . Với phương châm chia sẻ Bí quyết Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha.Example 14 - Chapter 3 Class 6 Playing with Numbers
Last updated Jan. 3, 2022 by
Nội dung chính- Example 14 - Chapter 3 Class 6 Playing with NumbersWhat is the least number which when divided by 12 14 and 16 leaves Aremainder of 7?What is the least number which when divided by 12 15 18 24 and 36 will leave 7 as remainder in each case?What is the least number which when divided by 12 24 and 30 leaves a remainder 7 in each case?Which is the least number which when divided by 12 16 36 and 18 leaves a remainder 3 in each case?



This video is only available for Teachoo black users
Solve all your doubts with Teachoo Black (new monthly pack available now!)
Transcript
Example 14 Find the least number which when divided by 12, 16, 24 and 36 leaves a remainder 7 in each case. Least number when divided by 12, 16, 24, 36 & leaves remainder 0 = LCM of 12, 16, 24, 36 So, LCM leaves remainder 0 Now, in the question We are asked smallest number which leaves remainder 7 So, Required number will be 7 more than LCM ∴ Required number = LCM + 7 Finding LCM of 12, 16, 24, 36 ∴ LCM = 2 × 2 × 2 × 2 × 3 × 3 = 16 × 9 = 144 So, Required Number = LCM + 7 = 144 + 7 = 151
`151``121``141``111`
Answer : A
Solution : To solve this question, we first have to find `LCM` of `12,16,24 and 36`.
`LCM` of these 4 numbers will be `144`. Please refer to video to find `LCM`.
So, least number that leaves remainder `7` when divided by `12, 16, 24 and 36` `= 144+7 = 151`
Knockout CUET (Physics, Chemistry and Mathematics)
Complete Study Material based on Class 12th Syllabus, 10000+ Question Bank, Unlimited Chapter-Wise and Subject-Wise Mock Tests, Study Improvement Plan.
₹ 7999/- ₹ 4999/-
Buy NowKnockout CUET (Physics, Chemistry and Biology)Complete Study Material based on Class 12th Syllabus, 10000+ Question Bank, Unlimited Chapter-Wise and Subject-Wise Mock Tests, Study Improvement Plan.
₹ 7999/- ₹ 4999/-
Buy NowKnockout JEE Main (Six Month Subscription)- AI Coach Study Modules, - Unlimited Mock Tests, - Study Improvement Plan.
₹ 9999/- ₹ 8499/-
Buy NowKnockout JEE Main (Nine Month Subscription)- AI Coach Study Modules, - Unlimited Mock Tests, - Study Improvement Plan.
₹ 13999/- ₹ 12499/-
Buy NowKnockout NEET (Six Month Subscription)- AI Coach Study Modules, - Unlimited Mock Tests, - Study Improvement Plan.
₹ 9999/- ₹ 8499/-
Buy NowFind the least number which when divided by 12, 16, 24 and 36 leaves a remainder 7 in each case.
SolutionWe first find the LCM of 12, 16, 24, and 36 as follows:
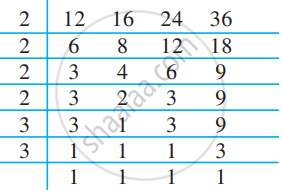
Thus, LCM = 2 × 2 × 2 × 2 × 3 × 3 = 144
144 is the least number which when divided by the given numbers will leave remainder 0 in each case. But
we need the least number that leaves remainder 7in each case.
Therefore, the required number is 7 more than 144.
The required least number = 144 + 7 = 151.
Concept: Lowest Common Multiple
Is there an error in this question or solution?
What is the least number which when divided by 12 14 and 16 leaves Aremainder of 7?
= 48 – 7 = 41. Hence option [C] is correct answer.What is the least number which when divided by 12 15 18 24 and 36 will leave 7 as remainder in each case?
Hence, the least required number = 360.What is the least number which when divided by 12 24 and 30 leaves a remainder 7 in each case?
So we add 7 to the LCM (144+7=151). Hence the smallest number that when divided by 12 16 24 and 36 leaves a remainder 7 is 151.Which is the least number which when divided by 12 16 36 and 18 leaves a remainder 3 in each case?
So, The Smallest number is 36 + 3 = 39 which leaves a remainder 3 when divided by 12 and 18. Tải thêm tài liệu liên quan đến nội dung bài viết Find the least number which when divided by 12,16,24 and 36 leaves a remainder 7 in each case
Post a Comment