Mẹo What would be the difference between the simple interest and the compound interest on a sum of money at the end of 4 years?
Mẹo Hướng dẫn What would be the difference between the simple interest and the compound interest on a sum of money the end of 4 years? 2022
Dương Khoa Vũ đang tìm kiếm từ khóa What would be the difference between the simple interest and the compound interest on a sum of money the end of 4 years? được Cập Nhật vào lúc : 2022-10-15 04:08:06 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha.Compound Interest: The future value (FV) of an investment of present value (PV) dollars earning interest an annual rate of r compounded m times per year for a period of t years is:
Nội dung chính- What is meant by Compound Interest?Compound Interest FormulaDerivation of Compound
Interest FormulaCompound Interest Formula for Different Time PeriodsCompound Interest Formula - Half YearlyCompound Interest Formula - Quarterly FAQs on Compound InterestHow to Calculate Compound Interest?What Is the Difference Between Simple and Compound Interest?How to Calculate Amount Using Compound Interest?How To Calculate Amount Using Compound Interest Formula? What Is the Monthly Compound Interest Formula? What Is the Daily Compound Interest Formula? What Is the Future Value Compound Interest Formula?Is Interest Compounded Daily Better than Monthly?What Are the Main Disadvantages of Compound
Interest?How Does Compound Interest Depend on Time Period?How Much is Compound Interest Greater than Simple Interest?Can Compound Interest be Greater than Principal?How Do you Calculate Compound Interest for Half Year?What Is the Information Required to Calculate Compound Interest?What Are the Units of
Compound Interest?What will be the difference between compound interest and simple interest for 4 years?What is the difference between simple interest and compound interest received on a sum of?What will be the difference between the compound interest and simple interest on a sum of rupees 6400 the rate of 10% per annum for 2 years?What is the difference between the simple interest and the compound interest on a sum of 8000 for 2.4 years the rate of 10% pa when the interest is compounded yearly?
FV = PV(1 + r/m)mtor
FV = PV(1 + i)n
where i = r/m is the interest per compounding period and n = mt is the number of compounding periods.
One may solve for the present value PV to obtain:
PV = FV/(1 + r/m)mt
Numerical Example: For 4-year investment of $20,000 earning 8.5% per year, with interest re-invested each month, the future value is
FV = PV(1 + r/m)mt = 20,000(1 + 0.085/12)(12)(4) = $28,065.30
Notice that the interest earned is $28,065.30 - $20,000 = $8,065.30 -- considerably more than the corresponding simple interest.
Effective Interest Rate: If money is invested an annual rate r, compounded m times per year, the effective interest rate is:
reff = (1 + r/m)m - 1.
This is the interest rate that would give the same yield if compounded only once per year. In this context r is also called the nominal rate, and is often denoted as rnom.
Numerical Example: A CD paying 9.8% compounded monthly has a nominal rate of rnom = 0.098, and an effective rate of:
r eff =(1 + rnom /m)m = (1 + 0.098/12)12 - 1 = 0.1025.
Thus, we get an effective interest rate of 10.25%, since the compounding makes the CD paying 9.8% compounded monthly really pay 10.25% interest over the course of the year.
Mortgage Payments Components: Let where P = principal, r = interest rate per period, n = number of periods, k = number of payments, R = monthly payment, and D = debt balance after K payments, then
R = P � r / [1 - (1 + r)-n]
andD = P � (1 + r)k - R � [(1 + r)k - 1)/r]
Accelerating Mortgage Payments Components: Suppose one decides to pay more than the monthly payment, the question is how many months will it take until the mortgage is paid off? The answer is, the rounded-up, where:
n = log[x / (x � P � r)] / log (1 + r)
where Log is the logarithm in any base, say 10, or e.Future Value (FV) of an Annuity Components: Ler where R = payment, r = rate of interest, and n = number of payments, then
FV = [ R(1 + r)n - 1 ] / r
Future Value for an Increasing Annuity: It is an increasing annuity is an investment that is earning interest, and into which regular payments of a fixed amount are made. Suppose one makes a payment of R the end of each compounding period into an investment with a present value of PV, paying interest an annual rate of r compounded m times per year, then the future value after t years will be
FV = PV(1 + i)n + [ R ( (1 + i)n - 1 ) ] / i where i = r/m is the interest paid each period and n = m � t is the total number of periods.
Numerical Example: You deposit $100 per month into an account that now contains $5,000 and earns 5% interest per year compounded monthly. After 10 years, the amount of money in the account is:
FV = PV(1 + i)n + [ R(1 + i)n - 1 ] / i =
5,000(1+0.05/12)120 + [100(1+0.05/12)120 - 1 ] / (0.05/12) = $23,763.28
Value of a Bond:
V is the sum of the value of the dividends and the final payment.
You may like to perform some sensitivity analysis for the "what-if" scenarios by entering different numerical value(s), to make your "good" strategic decision.
Replace the existing numerical example, with your own case-information, and then click one the Calculate.
Compound interest is an interest accumulated on the principal and interest together over a given time period. The interest accumulated on a principal over a period of time is also accounted under the principal. Further, the interest calculation for the next time period is on the accumulated principal value. Compound interest is the new method of calculation of interest used for all financial and business transactions across the world. The power of compounding can easily be understood, when we observe the compound interest values accumulated across successive time periods.
A sum of money of $100 invested over a period of time for a 10% rate would give a simple interest of $10, $10, $10... over successive time periods of 1 year, but would give a compound interest of $10, $11, $12.1, $13.31... Let us understand more about this, and the calculations of compound interest in the below content.
What is meant by Compound Interest?
Compound interest is the interest paid on both principal and interest, compounded regular intervals. At regular intervals, the interest so far accumulated is clubbed with the existing principal amount and then the interest is calculated for the new principal. The new principal is equal to the sum of the Initial principal, and the interest accumulated so far.
Compound Interest = Interest on Principal + Compounded Interest Regular Intervals
The compound interest is calculated regular intervals like annually(yearly), semi-annually, quarterly, monthly, etc; It is like, re-investing the interest income from an investment makes the money grow faster over time! It is exactly what the compound interest does to the money. Banks or any financial organization calculate the amount based on compound interest only.
Compound Interest Formula
The compound interest is calculated, after calculating the total amount over a period of time, based on the rate of interest, and the initial principal. For an initial principal of P, rate of interest per annum of r, time period t in years, frequency of the number of times the interest is compounded annually n, the formula for calculation of amount is as follows.

The above formula represents the total amount the end of the time period and includes the compounded interest and the principal. Further, we can calculate the compound interest by subtracting the principal from this amount. The formula for calculating the compound interest is as follows

In the above expression,
- P is the principal amountr is the rate of interest(decimal)n is frequency or no. of times the interest is compounded annuallyt is the overall tenure.
It is to be noted that the above-given formula is the general formula when the principal is compounded n number of times in a year. If the given principal is compounded annually, the amount after the time period percent rate of interest, r, is given as:
A = P(1 + r/100)t, and C.I. would be: P(1 + r/100)t - P .
Derivation of Compound Interest Formula
The formula for compound interest can be derived from the formula for simple interest. The formula for simple interest is the product of the principal, time period, and rate of interest (SI = ptr/100). Before looking into to derivation of the formula for compound interest, let us understand the basic difference between simple interest, compound interest computation. The principal remains constant over a period of time, for simple internet computation, but for compound interest computation the interest is added to the principal, for compound interest computation.
Derivation:
The derivation of the compound interest formula is given in the following steps:
- Let the principal be P and the rate of interest be R% per annum. Since the interest is compounded annually, so the compounding period is 1 year. It is to be noted that the principal (P) will
change after every 1 year. So, let us calculate the interest for the first year. The interest for the first year will be as follows:Let the interest for the first year be I1I1= R% of P = R/100 × PNow, the amount the end of the first year will be:A1 = P + I1 = P + (R/100 × P). This will give A1 = P (1 + R/100)Now, let us calculate the
interest for the second year. It is to be noted that the amount of the first year will become the Principal of the second year. Let this Principal be P2Now, P2 = A1 = P (1 + R/100)Now, let us take the interest for the second year to be I2 = R% of P2, which is R/100 × P2 = R/100 × P(1 + R/100)Now, the amount the end of the second year will be A2 = P2 +I2
which is P (1 + R/100) + R/100 × P(1 + R/100)This expression can be written as A2 =P (1 + R/100) (1 + R/100) = P (1 + R/100)2Continuing in this manner for n compounding periods, the amount the end of the nth compounding period can be expressed as A = P(1 + R/100)n. From the above formulas and computations, you can observe that the compound interest is the same as simple
interest for the first interval. But, over a period of time, there is a remarkable difference in returns.
The simple interest value for each of the years is the same, as the principal on which it is calculated is constant. But the compound interest is varying and increasing across the years. Because the principal on which the compound interest is calculated is increasing. The principal for a particular year is equal to the sum of the initial principal value, and the accumulated interest of the past years.
For example, a sum of $10,000 is deposited a rate of 10%. The below table explains the difference between simple interest and compound interest computation on this principal:
Simple Interest Calculation (r = 10%) Compound Interest Calculation(r = 10%)For 1st year:
P = 10,000
Time = 1 year
Interest = 1000
For 1st year:
P = 10,000
Time = 1 year
Interest = 1000
For 2nd year:
P = 10,000
Time = 1 year
Interest = 1000
For 2nd year:
P = 11000
Time = 1 year
Interest = 1100
For 3rd year:
P = 10,000
Time = 1 year
Interest = 1000
For 3rd year:
P = 12100
Time = 1 year
Interest = 1210
For 4th year:
P = 10,000
Time = 1 year
Interest = 1000
For 4th year:
P = 13310
Time = 1 year
Interest = 1331
For 5th year:
P = 10,000
Time = 1 year
Interest = 1000
For 5th year:
P = 14641
Time = 1 year
Interest = 1464.1
Total Simple Interest = 5000 Total Compount Interest = 6105.1 Total Amount = 1000 + 5000 = 6000 Total Amount = 1000 + 6105.1 = 7105.1Compound Interest Formula for Different Time Periods
Compound interest for a given principal can be calculated for different time periods using different formulas.
Compound Interest Formula - Half Yearly
The interest in the case of compound interest varies based on the period of computation. If the time period for the calculation of interest is half-yearly, the interest is calculated every six months, and the amount is compounded twice a year.
The formula to calculate the compound interest when the principal is compounded semi-annually or half-yearly is given as:

Here the compound interest is calculated for the half-yearly period, and hence the rate of interest r, is divided by 2 and the time period is doubled. The formula to calculate the amount when the principal is compounded semi-annually or half-yearly is given by:
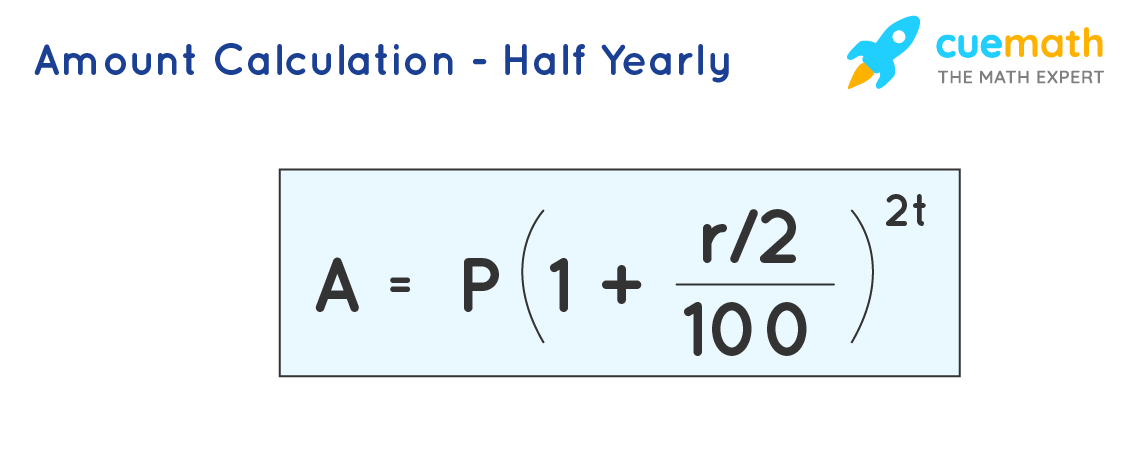
In the above expression,
- A is the amount the end of the time periodP is the initial principal
value, r is the rate of interest per annumt is the time periodC.I. is the compound interest.
Compound Interest Formula - Quarterly
If the time period for the calculation of interest is quarterly, the interest is calculated for every three months, and the amount is compounded 4 times a year. The formula to calculate the compound interest when the principal is compounded quarterly is given as:

Here the compound interest is calculated for the quarterly time period, and hence the rate of interest r, is divided by 4 and the time period is quadrupled. The formula to calculate the amount when the principal is compounded quarterly is given by:

In the above expression,
- A is the amount the end of the time periodP is the initial principal value, r is the rate of interest per annumt is the time periodC.I. is the compound interest.
Monthly Compound Interest Formula
The
monthly compound interest formula is also known as the interest calculated per month i.e., n = 12. Total compound interest is the final amount excluding the principal amount. The monthly compound interest formula is expressed as:
CI = P (1 + r/12)12t - P
Daily Compound Interest Formula
When the amount compounds daily, it means that
the amount compounds 365 times in a year. i.e., n = 365. The daily compound interest formula is expressed as:
CI = P (1 + r/365)365t - P
Important Notes
Compound interest depends on the amount accumulated the end of the previous tenure but not on the original principal. Banks, insurance companies, etc. generally levy compound interest.If the interest is compounded quarterly, the formula of amount is given by:beginequationA=Pleft(1+fracr / 4100right)^4 nendequation While calculating the compound interest, the rate of interest, and each time period must be of the same duration.Tips & Tricks
- The rule of 72: It is a quick
method to know how long it will take for your money to double. Doubling Time = 72/Interest Rate
Using the rule of 72, we can find the number of years to double your money by simply dividing 72 by the rate of interest. For example, an 8% compounded interest rate your money will double in 72 ÷ 8 = 9The time duration over which an interest rate is applicable is referred to in many different terms. Sometimes it is called “per annum” or “annual” or “per year”. All of these mean you’ll get the given rate of interest over a period of 1 year. Semi-annual is 6 months. While quarterly is 3 months duration.
FAQs on Compound Interest
How to Calculate Compound Interest?
The formula used to calculate compound interest is CI = P( 1 + r/100)n - P. Here in this formula the amount is calculated and then the principal is subtracted from it, to obtain the compound interest value.
What Is the Difference Between Simple and Compound Interest?
Simple interest is the interest paid only on the principal, whereas, compound interest is the interest paid on both principal and interest compounded regular intervals.
How to Calculate Amount Using Compound Interest?
There is a direct formula for the calculation of compound interest. A = P(1 + r/100)n. Here we need to define the rate of interest and the time interval which the compound interest is calculated.
How To Calculate Amount Using Compound Interest Formula?
There is a general compound interest formula for the calculation of compound interest i.e.,
CI = Amount - Principal
where, Amount = P(1 + r/100)t. By substituting the given parameters such as P
(principal amount), r (rate of interest), and t (time) amount can be easily calculated.
What Is the Monthly Compound Interest Formula?
The monthly compound interest formula is given as
CI = P(1 + (r/12) )12t - P. Where, P is the principal amount, r is the interest rate in decimal form, n = 12 (it means that the amount compounded 12 times in a year), and t is the time.
What Is the Daily Compound Interest Formula?
The
daily compound interest formula is given as
A = P (1 + r / 365)365 t, where P is the principal amount, r is the interest rate of interest in decimal form, n = 365 (it means that the amount compounded 365 times in a year), and t is the time.
What Is the Future Value Compound Interest Formula?
The future value compound interest formula is expressed as FV = PV (1 + r / n)n t. Here, PV = Present Value (Initial investment), r = rate of interest, n = number of times the amount is compounding, and t = time in years.
Is Interest Compounded Daily Better than Monthly?
The interest compounded daily has 365 compounding cycles a year. It will generate more money compared to interest compounded monthly, which has only 12 compounding cycles per year.
What Are the Main Disadvantages of Compound Interest?
If we miss a payment by a day also, towards the end of tenure it may incur a huge loss. The interest calculation is for the next cycle and for a higher value. Compound interest is actually designed to help the lenders but not the borrowers.
How Does Compound Interest Depend on Time Period?
The compound interest depends on the time interval of calculation of interest. The time interval for the calculation of interest can be a day, a week, month, quarterly, half-yearly. For the shorter time period of calculation, the net accumulated compound interest is higher.
How Much is Compound Interest Greater than Simple Interest?
The compound interest can be greater than the simple interest. The compound interest value varies and increases for successive time periods. An initial principal of $100 invested over a period of time would give a simple interest of $10, $10, %10... over successive time periods of 1 year, but would give a compound interest of $10, $11, $12.1, $13.31..... Thus the compound interest is greater than the simple interest. Only for the first year, or for the first cycle of calculation, the compound interest, and the simple interest values are equal.
Can Compound Interest be Greater than Principal?
The compound interest can be greater than the principal. The compound interest value varies and increases for successive time periods. An initial principal of $100 invested over a period of time would give a compound interest of $10, $11, $12.1, $13.31....over successive time periods of 1 year each. Thus the compound interest increases over a period of time and can be greater than the initial principal value.
How Do you Calculate Compound Interest for Half Year?
The formula for calculation of compound interest for half year is CI = p(1 + r/2/100)2t.- p. Here in this formula 'A' is the final amount, 'p' is the principal, and 't' is the time in years. In the formula we can observe that the rate of interest is halved and the time is doubled, to account for the calculation of compound interest for half a year.
What Is the Information Required to Calculate Compound Interest?
The calculation of compound interest requires us to know the principal, rate of interest, and the time period. Also, we need to know the time interval for which the interest is to be calculated.
What Are the Units of Compound Interest?
The units of compound interest are the unit of currency and are the same as the unit used for the principal value. If the principal is in dollars, or yen, the compound interest would also be in dollars or yen.
What will be the difference between compound interest and simple interest for 4 years?
SI for the 4th yr = SI for the 1st yr = 0.2P . So, diff. betn CI and SI for 4th yr = 0.3456P - 0.2P = 0.1456P .What is the difference between simple interest and compound interest received on a sum of?
The major difference between simple interest and compound interest is that simple interest is based on principal amount whereas compound interest is based on the principal amount and the interest compounded for a cycle of the period.What will be the difference between the compound interest and simple interest on a sum of rupees 6400 the rate of 10% per annum for 2 years?
The simple interest is given as S I = P r t 100 and the compound interest is given as C I = P ( 1 + r 100 ) t − P where P is the prinicipal amount, r is the interest rate and t is the time in years. Hence D is the correct answer. ∴ Required difference = 1% of 6400 = 6400 × (1/100) = 64.What is the difference between the simple interest and the compound interest on a sum of 8000 for 2.4 years the rate of 10% pa when the interest is compounded yearly?
Answer: The difference between the simple interest and compound interest is Rs 80 . sum of Rs 8000 lent 10% p.a. in 2 years. Tải thêm tài liệu liên quan đến nội dung bài viết What would be the difference between the simple interest and the compound interest on a sum of money the end of 4 years? What is compounding Simple interest example Compound interest example Compounded annually Compound interest math
Post a Comment