Review What is the total number of functions that can be defined from the set 12 to the set 1 2 3?
Mẹo Hướng dẫn What is the total number of functions that can be defined from the set 12 to the set 1 2 3? Chi Tiết
Dương Văn Hà đang tìm kiếm từ khóa What is the total number of functions that can be defined from the set 12 to the set 1 2 3? được Update vào lúc : 2022-09-28 04:08:05 . Với phương châm chia sẻ Kinh Nghiệm Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha.Nội dung chính
-
The number of one-one functions that can be defined from set a, b, c, d to the set 1, 2, 3, 4 is?
The number of one-one functions that can be defined from A = 4, 8, 12, 16 to B is 5040, then n(B)=a). 7b). 8c). 9d). 10
Solved Examples – Number Of FunctionsFrequently Asked QuestionsHow do you find the number of functions?How do you calculate the number of injective
functions?How do you calculate the number of bijective functions?What do you mean by one to one function?What is the total number of function that can be defined from the set 12 to the set 1 2 3?What is the total number of functions that can be defined from the set?What is the total number of functions defined from A to B if'n A 2 and N B 3?How many onto functions are there from a set with 5 elements to a set with 4 elements?
The number of one-one functions that can be defined from set a, b, c, d to the set 1, 2, 3, 4 is?
Answer
Verified
Hint: Use the cardinality of two sets to find the number of one-one functions between them.
[textNumber of one-one functions = ^nP_mtext if nge textm]…..(1)
Number of one-one functions = 0 if n < m…..(2)Complete step-by-step answer:
The total number of elements in the set is called the cardinality of the set.
Let us assume given sets as A and B, that is,
A = a, b, c, d and B = 1, 2, 3, 4
The cardinality of a set is denoted by
“|set|”
Here cardinality of A = |A| = 4.
Cardinality of B = |B| = 4.
If there are two non-empty sets with cardinality m and n, then the number of one-one functions between them is given by:
[textNumber of one-one functions = ^nP_mtext if nge textm] …..(1)
Number of one-one functions = 0 if n < m…..(2)
By the above formula, in our case the value of m is 4 and the value of n is 4.
We can see that m = n.
So we need to use equation
(1):
[textNumber of one-one functions = ^nP_mtext if nge textm].
So, the number of one-one functions = [^4P_4]
By using the formula,
[^nP_m=dfracn!left( n-m right)!]
By substituting factorial of 0 as 1,we get:
[textThe number of one-one functions =^4P_4=dfrac4!(4-4)!=4!] [$because$ 0!=1]
The number of one-one functions = (4)(3)(2)(1) = 24.
[therefore ]The total number of one-one functions from a,
b, c, d to 1, 2, 3, 4 is 24.
Note: Here the values of m, n are same but in case they are different then the direction of checking matters. If m > n, then the number of one-one from first set to the second becomes 0. So take care of the direction of checking.
The number of one-one functions that can be defined from A = 4, 8, 12, 16 to B is 5040, then n(B)=a). 7b). 8c). 9d). 10
Answer
Verified
Hint: For solving this problem, we first find the number of elements given for set A. The number of one-one functions from A to B is 5040. Let the number of elements in B be n. Now by applying the formula for one-one functions that is $^nP_m$, we can obtain the number of elements in B.Complete step-by-step solution -
A function as is said to be a one-one function or an injection, if different elements of A have different images in B. If A and B are finite sets having m
and n elements respectively such that m is less than equal to n, then to define a one-one function from A to B, we have to relate m elements in A to n distinct elements in B. Thus, number of one-one function: $^nP_m$.
According to our problem we are given that the number of functions that can be defined from A to B is 5040. The number of elements in A are 4. We are required to find the number of elements in B. By using the above formula and putting m = 4 and n same, we get
$
Rightarrow ^nP_m=5040 \ $
$ Rightarrow ^nP_4=5040 \ $
From the definition of permutation, $^nP_r=dfracn!left( n-r right)!$
On expanding further, we get
$Rightarrow ^nP_4=dfracn!left( n-4 right)! \ $
$Rightarrow dfracn!left( n-4 right)!=5040 \ $
As, we know $ ^10P_4=5040 \ $
$Rightarrow dfracn!left( n-4 right)!=dfrac10!left( 10-4 right)! \ $
$ therefore n=10 \ $
Therefore, there are 10 elements present in B.
Hence, option (d) is correct.
Note: Another possible method to solve this problem can be explained as: Let the first element 4 in A be mapped on n elements of B. Similarly, the second element 8 is mapped on (n -1) elements. Hence, we can write for four elements mapping as: $nleft( n-1 right)left( n-2 right)left( n-3 right)=5040$. Putting n as 10, we get the same result.
Number of functions is an important topic in sets. A relation in which each input has a particular output is called a function. If f is a function from set A to set B, then each element of A will be mapped with only one element in B. In this article, we come across the formula to find the number of functions from given sets and some solved examples.
Consider a set X having 6 elements and another set Y having 5 elements. Every element of set X will be mapped to one element in set Y. So each element of X has 5 elements to be chosen from. Hence, the total number of functions will be 5×5×5.. 6 times = 56.
1. Number of possible functions
If a set A has m elements and set B has n elements, then the number of functions possible from A to B is nm.
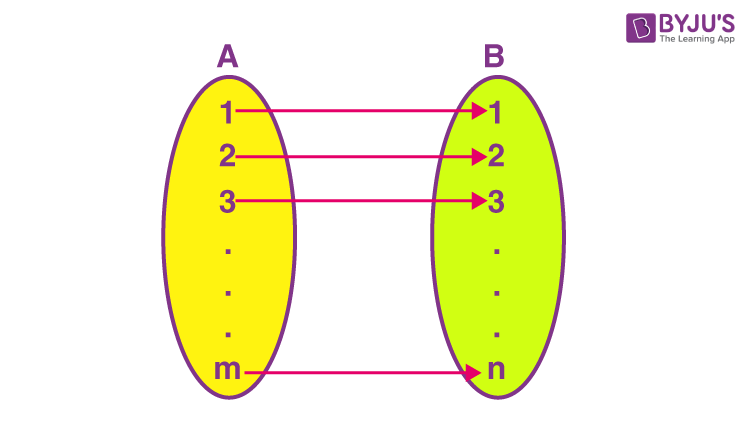
For example, if set A = 3, 4, 5, B = a, b.
The total number of possible functions from A to B = 23 = 8
2. Number of Surjective Functions (Onto Functions)
If a set A has m elements and set B has n elements, then the number of onto functions from A to B = nm – nC1(n-1)m + nC2(n-2)m – nC3(n-3)m+….- nCn-1 (1)m.
Note that this formula is used only if m is greater than or equal to n.
For example, in the case of onto function from A to B, all the elements of B should be used. If A has m elements and B has 2 elements, then the number of onto functions is 2m-2. From a set A of m elements to a set B of 2 elements, the total number of functions is 2m. In these functions, 2 functions are not onto (If all elements are mapped to 1st element of B or all elements are mapped to 2nd element of B). So, the number of onto functions is 2m-2.
3. Number of Injective Functions (One to One)
If set A has n elements and set B has m elements, m≥n, then the number of injective functions or one to one function is given by m!/(m-n)!.
4. Number of Bijective functions
If there is bijection between two sets A and B, then both sets will have the same number of elements. If n(A) = n(B) = m, then number of bijective functions = m!.
Solved Examples – Number Of Functions
Example 1:
The number of onto functions from set P = a, b, c, d to set Q. = u, v, w is:
(A) 68
(B) 36
(C) 81
(D) 64
Solution:
P = a, b, c, d
Q. = u, v, w
Here n(P) = m = 4
n(Q.) = n = 3
The number of onto functions = 34 – 3C1(3-1)4 + 3C2(3-2)4
= 81 – 48 + 3
= 36.
Hence, option B is the answer.
Example 2:
The number of bijective functions from set A to itself when A contains 106 elements is
(A) 106
(B) 106!
(C) 1062
(D) 2106
Solution:
n(A) = m = 106
The number of bijective functions = m!
= 106!
Hence, option B is the answer.
Related video

Frequently Asked Questions
How do you find the number of functions?
Let set A has p elements and set B has q elements, then the number of functions possible from A to B is qp.
How do you calculate the number of injective functions?
If n(A) = n and n(B) = m, m≥n, then the number of injective functions or one to one functions is given by m!/(m-n)!.
How do you calculate the number of bijective functions?
If n(A) = n(B) = p, then the number of bijective functions = p!.
What do you mean by one to one function?
A function is one-to-one if every element of the range of the function corresponds to exactly one element of the domain of the function.
What is the total number of function that can be defined from the set 12 to the set 1 2 3?
Solution : The total number of functions that can be defined from the set 1,2 to the set 1,2,3 is `3^2=9`.What is the total number of functions that can be defined from the set?
If a set A has m elements and set B has n elements, then the number of functions possible from A to B is nm. For example, if set A = 3, 4, 5, B = a, b. If a set A has m elements and set B has n elements, then the number of onto functions from A to B = nm – nC1(n-1)m + nC2(n-2)m – nC3(n-3)m+…. - nCn-1 (1)m.What is the total number of functions defined from A to B if'n A 2 and N B 3?
Answer. Hence , the answer is 64.How many onto functions are there from a set with 5 elements to a set with 4 elements?
Total onto function can be formed =35−3−3×25=144. Tải thêm tài liệu liên quan đến nội dung bài viết What is the total number of functions that can be defined from the set 12 to the set 1 2 3?
Post a Comment