Review Cho hình chóp sabcd có ABCD là hình vuông tâm O và SA vuông góc với ABCD tam giác BCD là
Kinh Nghiệm về Cho hình chóp sabcd có ABCD là hình vuông vắn tâm O và SA vuông góc với ABCD tam giác BCD là Mới Nhất
Bùi Ngọc Chi đang tìm kiếm từ khóa Cho hình chóp sabcd có ABCD là hình vuông vắn tâm O và SA vuông góc với ABCD tam giác BCD là được Cập Nhật vào lúc : 2022-09-06 20:02:02 . Với phương châm chia sẻ Bí quyết về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha.Giới thiệu về cuốn sách này
Nội dung chính- CÂU HỎI KHÁCD. Tam giác vuông Tam giác SBC là tam giác vuông tại B vì : AB là hình chiếu của SB trên (ABCD),
mà BC ⊥ AB (do ABCD là hình vuông vắn)
⇒ BC ⊥ SB (theo định lí ba đường vuông góc)
⇒ tam giác SBC là tam giác vuông
Đáp án D CÂU HỎI HOT CÙNG CHỦ ĐỀVideo liên quan
Giới thiệu về cuốn sách này
- lý thuyết trắc nghiệm hỏi đáp bài tập sgk
Cho hình chóp S.ABCD, có đáy là hình vuông vắn tâm O. SA ⊥ (ABCD). Gọi H, I, K lần lượt là hình chiếu vuông góc của A trên SB, SC, SD.
a) CMR : BC ⊥ (SAB), CD ⊥ (SAD), BD ⊥ (SAC)
b) CMR : AH, AK cùng vuông góc với SC. Từ đó suy ra 3 đường thẳng AH, AI, AK cùng nằm trong một mặt phẳng.
c) CMR : HK ⊥ (SAC). Từ đó suy ra HK ⊥ AI.
Các thắc mắc tương tự
Cho hình chóp S ABCD, có đáy là hình vuông vắn tâm O, SA vuông góc với mặt phẳng (ABCD). Gọi H, I, K lần lượt là hình chiếu vuông góc của điểm A lên SB, SC, SD.
1.CMR : AH, AK cùng vuông góc với SC. Từ đó suy ra 3 đường thẳng AH, AI, AK cùng nằm trong một mặt phẳng.
2. Chứng minh rằng HK⊥(SAC) , HK ⊥ AI.
Cho hình chóp S.ABCD có đáy là hình vuông vắn tâm O, AB = SA = a, SA vuông góc với (ABCD). Gọi (P) là mặt phẳng qua A và vuông góc với SC, (P) cắt SB, SC, SD lần lượt tại H, I, K.
a, Chứng minh HK // BD.
b, Chứng minh AH vuông góc với SB, AK vuông góc với SD.
c, CM tứ giác AHIK có 2 đường chéo vuông góc. Tính diện tích s quy hoạnh AHIK theo a.
Mình không xác định được mp (P) nên giúp mình vẽ cả hình nữa nhé! Cảm ơn nhiều.
Cho hình chóp S.ABCD, đáy ABCD là hình vuông vắn; SA(perp)(ABCD).
a, Chứng minh những (Delta SBC,SDC) là những (Delta) vuông.
b, Từ A kẻ AH(perp)SB, AK(perp)SC, AI(perp)SD. Chứng minh 3 đường thẳng AH, AK, AI đồng phẳng.
c, Chứng minh HI(perp)AK
d, Biết (AB=a,SA=asqrt2). Tính (S_AHKI) theo a
- lý thuyết trắc nghiệm hỏi đáp bài tập sgk
Cho hình chóp S.ABCD có đáy là hình vuông vắn tâm O, SA vuông góc (ABCD). a) CM : BC vuông góc (SAB) và những mặt bên của hình chóp là những tam giác vuông. b) Gọi H,K là hình chiếu của A trên SB và SO. C/M : AH vuông góc SC va AK vuông góc BD c) C/M : K là trực tâm tam giác SBD
Các thắc mắc tương tự
Cho hình chóp S ABCD, có đáy là hình vuông vắn tâm O, SA vuông góc với mặt phẳng (ABCD). Gọi H, I, K lần lượt là hình chiếu vuông góc của điểm A lên SB, SC, SD.
1.CMR : AH, AK cùng vuông góc với SC. Từ đó suy ra 3 đường thẳng AH, AI, AK cùng nằm trong một mặt phẳng.
2. Chứng minh rằng HK⊥(SAC) , HK ⊥ AI.
Cho hình chóp S.ABCD có đáy là hình vuông vắn tâm O, AB = SA = a, SA vuông góc với (ABCD). Gọi (P) là mặt phẳng qua A và vuông góc với SC, (P) cắt SB, SC, SD lần lượt tại H, I, K.
a, Chứng minh HK // BD.
b, Chứng minh AH vuông góc với SB, AK vuông góc với SD.
c, CM tứ giác AHIK có 2 đường chéo vuông góc. Tính diện tích s quy hoạnh AHIK theo a.
Mình không xác định được mp (P) nên giúp mình vẽ cả hình nữa nhé! Cảm ơn nhiều.
Cho hình chóp (S.ABCD) có đáy là hình vuông vắn tâm (O) cạnh (1). Cạnh bên (SA) vuông góc với đáy và tam giác (SBD) đều. biết khoảng chừng cách giữa (SO,,,CD) bằng (dfracsqrt a b) trong đó (a,,,b) là những số tự nhiên. Khi đó giá trị của (a + b) là:
A.
B.
C.
D.
Bằng cách đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách Bảo mật của chúng tôi.
Hình chóp S.ABCD có đáy là hình vuông vắn ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Bài 3.31 trang 153 Sách bài tập (SBT) Hình học 11 – Bài 4. Hai mặt phẳng vuông góc
Hình chóp S.ABCD có đáy là hình vuông vắn ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Giả sử (left( alpha right)) là mặt phẳng đi qua A và vuông góc với cạnh SC, (left( alpha right)) cắt SC tại I.
a) Xác định giao điểm K của SO với mặt phẳng (left( alpha right)).
b) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) và (BrmDparallel left( alpha right)).
c) Xác định giao tuyến d của mặt phẳng (SBD) và mặt phẳng (left( alpha right)). Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng (left( alpha right)).
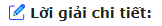
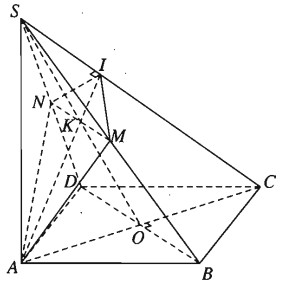
a) Gọi I là giao điểm của mặt phẳng (left( alpha right)) với cạnh SC. Ta có (left( alpha right) bot SC,AI subset left( alpha right) Rightarrow SC bot AI). Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và (AI subset left( alpha right)), nên K là giao điểm của SO với (left( alpha right)).
Quảng cáob) Ta có
(left. matrix BrmD bot AC hfill cr
BrmD bot SA hfill cr right} Rightarrow BrmD bot left( SAC right))
( Rightarrow BrmD bot SC)
Mặt khác (BrmD subset left( SBrmD right)) nên (left( SBrmD right) bot left( SAC right)).
Vì (BrmD bot SC) và (left( alpha right) bot SC) nhưng BD không chứa trong (left( alpha right)) nên (BrmDparallel left( alpha right))
Ta có (K = SO cap left( alpha right)) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (left( alpha right)) và (SBD). Mặt phẳng (SBD) chứa (BrmDparallel left( alpha right)) nên cắt theo giao tuyến (dparallel BrmD). Giao tuyến này đi qua K là vấn đề chung của (left( alpha right)) và (SBD). Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.
Mã thắc mắc: 46776
Loại bài: Bài tập
Chủ đề :
Môn học: Toán Học
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, nhấn vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
19/06/2022 795
D. Tam giác vuông
Đáp án đúng chuẩn
Tam giác SBC là tam giác vuông tại B vì : AB là hình chiếu của SB trên (ABCD), mà BC ⊥ AB (do ABCD là hình vuông vắn) ⇒ BC ⊥ SB (theo định lí ba đường vuông góc) ⇒ tam giác SBC là tam giác vuông Đáp án D
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Cho hình chóp S.ABCD, đáy là hình thoi tâm O và SA = SC, SB = SD
Đường thẳng AC vuông góc với mặt phẳng
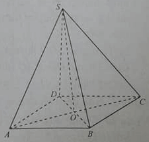
Xem đáp án » 19/06/2022 2,038
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Gọi M là trung điểm của AD và K là trung điểm của BD
Góc giữa CM với mặt phẳng (BCD) là:
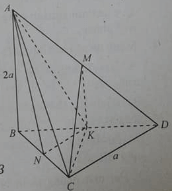
Xem đáp án » 19/06/2022 1,119
Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng 60o. Gọi M, N là trung điểm của AB và CD.
Đường thẳng CD vuông góc với mặt phẳng
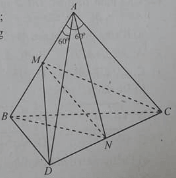
Xem đáp án » 19/06/2022 485
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa AC với mặt phẳng (ABD) bằng:
Xem đáp án » 19/06/2022 327
Tập hợp những điểm cách đều ba đỉnh của tam giác ABC là:
Xem đáp án » 19/06/2022 294
Cho hình tứ diện ABCD có ba cạnh AB, BC, CD đôi một vuông góc.
Đường thẳng AB vuông góc với :
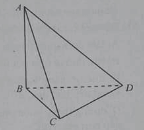
Xem đáp án » 19/06/2022 234
Cho hình chóp S.ABCD có ABCD là hình vuông vắn và SA ⊥ (ABCD) Tam giác SOD là:
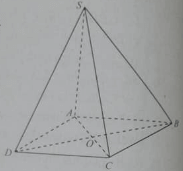
Xem đáp án » 19/06/2022 198
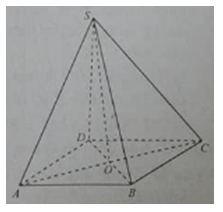
Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD. Đường thẳng BC vuông góc với đường thẳng
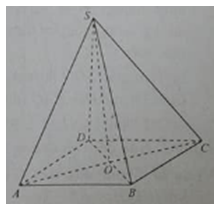
Xem đáp án » 19/06/2022 175
Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD. Đường thẳng DB không vuông góc với đường thẳng nào sau đây?
Xem đáp án » 19/06/2022 162
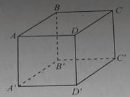
Cho hình lập phương ABCD. A’B’C’D’. AC vuông góc với mặt phẳng.
Xem đáp án » 19/06/2022 154
Cho một điểm S có hình chiếu H trên mặt phẳng (P). Với hai điểm M và N trong (P) sao cho SM ≤SN, ta có:
Xem đáp án » 19/06/2022 124
Cho hình lập phương ABCD. A’B’C’D’. Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:
Xem đáp án » 19/06/2022 110
Mặt phẳng trung trực của đoạn thẳng AB:
Xem đáp án » 19/06/2022 109
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa CM với mặt phẳng (BCD) bằng:
Xem đáp án » 19/06/2022 99
Cho một điểm S có hình chiếu H trên mặt phẳng (P). Với điểm M bất kì trong (P) ta có:
Xem đáp án » 19/06/2022 99
Tải thêm tài liệu liên quan đến nội dung bài viết Cho hình chóp sabcd có ABCD là hình vuông vắn tâm O và SA vuông góc với ABCD tam giác BCD là

Post a Comment