Review Cách tính diện tích xung quanh hình chóp đều
Mẹo về Cách tính diện tích s quy hoạnh xung quanh hình chóp đều Chi Tiết
Lê Hải Hưng đang tìm kiếm từ khóa Cách tính diện tích s quy hoạnh xung quanh hình chóp đều được Update vào lúc : 2022-09-24 14:02:03 . Với phương châm chia sẻ Mẹo về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Mình lý giải và hướng dẫn lại nha.§8. DIỆN TÍCH XUNG QUANH CỦA HÌNH CHÓP ĐỂU A. Tóm tốt kiến thức và kỹ năng - Diện tích xung quanh của hình chóp đều bằng tích cứa nửa chu vi đáy với trung đoạn : (p là nửa chu vi đáy ; d là trung đoạn) - Diện tích toàn phần của hình chóp bằng tống của diện tích s quy hoạnh xung quanh với diện tích s quy hoạnh đáy. B. Ví dụ giải toán Ví dụ Cho hình chóp tam giác đều S.ABC, BC = 6cm, đường cao so có độ dài Vó cm. Tính diện tích s quy hoạnh xung quanh và diện tích s quy hoạnh toàn phần cúa hình chóp đó. Giúi: Vì \BC là lam giác đều nên diem o là giao diêm cua ba dường trung luyến. Ta có OM = ị ÁM = ~~ 7 7 Coi 1 là trung diem cua BC thì SM BC. S.M là trung đoạn cua hình chóp dêu. Xét sol vuòng tại o. có SM = ựso' + OM' = /9 = 3 (em). Vá chẹn tích xung quanh cua hình chóp dó là : s, : p.d = ị:6.3.3 = 27 (em2). Diện tích toàn phan cua hình chóp là : 62 r- • s„, = 27 + ' = 27+ 9/? (cm2). 4 Nhặn xét : Diện tích xung quanh của hình chóp đều bằng nưa chu VI dày nhàn vói trung đoạn chứ không phai băng chu vi đáy nhan vói chiếu cao cua hình chóp. Bạn phai can than keo lầm 1 c. Hướng dân giải những bài tạp trong sách giáo khoa Bài 40. Giui SM = v252 -152 = 20 (em). Diện tích xung quanh cua hình chóp là : Sv„ = ị .30.4.20 = 1200 tem2). q ọ Diên tích toàn phần là : s„, = 1200 + 30.30 = 2100 (em2). Bài 41. G7(Z/. a) Trong hình có bốn tam giác cân bàng nhau (c.c.c). b) Chiêu cao ứng vói đáy cùa mỗi tam giác là : ỢlO2-2,52 = ^93,75 =9,68 (cm) . C) Diện tích xung quanh của hình chóp là : S ,, = 4 .5.4.9,68 = 96,8 (cm2) Diện tích toàn phan là : SIp = 96,8 + 25 = 121,8 (cm2). Bài 42. Hiáínĩ’ ihỉn Tính dường chéo cua lỉmh,vuông đáy rồi tính nửa đường 5y/ĩ. chéo được ——cm. Dùng dinh lí Pv-ta-go tính dường cao được 9,35cm. 2 . c- Bài 43. Giíii: Hình a) : sx„ = 1.20.4.20 = 800 (cm2). s,p = 800 + 20.20 = 1200 (cm2). Hình b) : Sxq = 1.7.4.12 = 168 (cm2). s,p = 168+ 7.7 = 217 (cm2). Hình c) : Trung đoạn SI = x/l 72 -82 = 15 (cm). Sx = — . 16.4.15 = 480 (cm2). 1 ọ s,n =480 + 16.16 = 736 (cm2). D. Bài tạp luyện thêm Cho hình chóp tam giác đều, cạnh hên sc = 17cm, trung đoạn SM = 15cm. Tính diện tích s quy hoạnh xung quanh cua hình chóp đó. Một hình chóp tam giác đều, cạnh đáy bằng 8cm, những mặt bên là những tam giác vuông cân. Tính diện tích s quy hoạnh toàn phần của hình chóp dó. Một hình chóp tứ giác đều, những mật bôn là những lam giác đều. Biết diện tích s quy hoạnh xung quanh là 9/3cm2, tính diện tích s quy hoạnh toàn phần. Ị Ị ưứnỊỊ (làn - t)áp sá Tính MC dược 8cm. BC = 1.6cm. i)('íỊ> .Sơ . 480cin . Xét ASBC vuông cán lụi s. Vì BC = Sem nên sĩ - 4cm. s .8.3.4. = 48 (cm2). st| 'Ị S„.=4S+ 4 Diên tích đáy là 9cm2. Slp = 993 + 9 = 9(V? + 1) (cm2).
Nội dung chính- Hình chóp là gì?Tính chất của hình chóp:Các quy mô chóp thường gặpHình chóp tam giác đều là gì?Hình chóp tứ giác đều là gì?Hình chóp cụt đều là gì?Công thức tính chu vi, diện tích s quy hoạnh, thể tích hình chópCông thức tính chu vi hình chóp (Áp dụng cho hình chóp tam giác, hình chóp tứ giác)Công thức tính diện tích s quy hoạnh hình chóp đều (Áp dụng cho hình chóp tam giác, hình chóp tứ giác)Thể tích hình chóp (Áp dụng cho hình chóp tam giác, hình chóp tứ giác)Thể tích hình chóp cụt 4 cạnhPhân biệt những hình chópDạng bài tập về hình chópVideo liên quan
Hình chóp nói chung và hình chóp tứ giác đều nói riêng là phần kiến thức và kỹ năng hình học trong chương trình toán lớp 8, học kì 2. Dưới đây là tổng kết về định nghĩa hình chóp là gì, tính chất, công thức tính chu vi, diện tích s quy hoạnh, thể tích những hình chóp thế nào?. Bên cạnh đó, chúng tôi có tương hỗ update thêm kiến thức và kỹ năng về những hình chóp ít được nhắc tới trong sách giáo khoa.
Đang xem: Công thức tính diện tích s quy hoạnh xung quanh hình chóp

Công trình vĩ đại của quả đât Kim tự tháp Ai Cập là hình chóp tam giác
Hình chóp là gì?
Định nghĩa”
Hình chóp là hình học không khí xuất hiện đáy là đa giác lồi và những mặt bên đều là tam giác có chung một đỉnh, đỉnh này gọi là đỉnh của hình chópHình chóp có nhiều loại rất khác nhau, tên của nó được quy định dựa theo đáy.Hình chóp tam giác có đáy là hình tam giác, hình chóp tứ giác có đáy là hình tứ giác.Trong những trường hợp đặc biệt như đáy là tam giác đều, tứ giác đều thì ta gọi đó là hình chóp đều
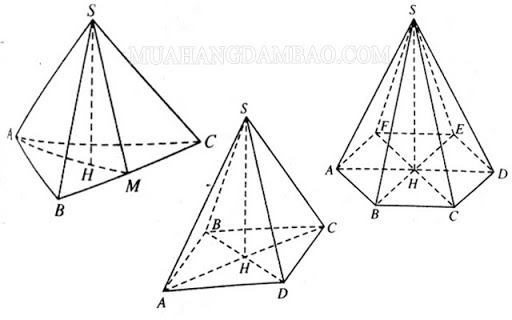
Định nghĩa hình chóp là gì?
Tính chất của hình chóp:
Đường thẳng đi qua một đỉnh và vuông góc với mặt phẳng đáy được gọi là đường cao của hình chóp.Tên gọi của hình chóp nhờ vào đa giác mặt đáy: hình chóp có đáy là tam giác được gọi là hình chóp tam giác, hình chóp có đáy là tứ giác gọi là hình chóp tứ giác.Nếu hình chóp có cạnh bên phù phù hợp với mặt đáy những góc bằng nhau hoặc những cạnh bên bằng nhau thì chân đường cao đó đó là tâm đường tròn ngoại tiếp đáy.Nếu hình chóp có những mặt bên phù phù hợp với mặt đáy những góc bằng nhau hoặc có những đường cao của những mặt bên xuất phát từ 1 đỉnh bằng nhau thì chân đường cao là tâm đường tròn nội tiếp mặt đáy.Nếu hình chóp xuất hiện bên hoặc mặt chéo vuông góc với mặt phẳng đáy thì đường cao của hình chóp sẽ là đường cao của mặt bên hoặc mặt chéo đó.
Các quy mô chóp thường gặp
Hình chóp tam giác đều là gì?
*Định nghĩa:
Hình chóp tam giác đều là hình chóp có đáy là tam giác đều, những mặt bên là những tam giác cân đối nhau có chung đỉnh
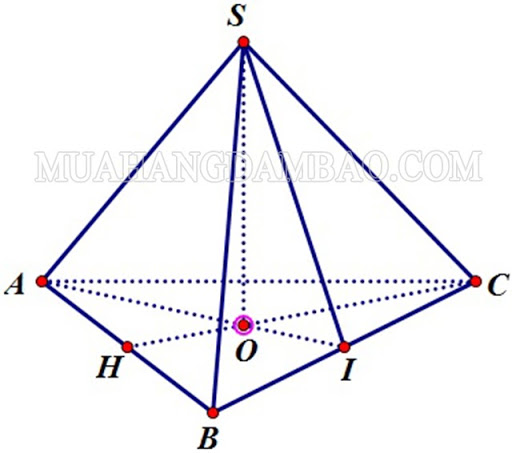
Hình chóp SABC có đáy là tam giác đều – Hình chóp tam giác đều
*Tính chất
Hình chóp tam giác đều có 3 mặt phẳng đối xứngHình chóp có đáy là tam giác đềuCác cạnh bên bằng nhauTất cả những mặt bên là những tam giác cân đối nhauChân đường cao trùng với tâm của mặt đáy (tâm đáy là trọng tâm của tam giác)Tất cả những góc tạo bởi những mặt bên và mặt đáy đều bằng nhauTất cả những góc tạo bởi cạnh bên và mặt đáy đều bằng nhau
***Lưu ý:
Tâm của tam giác đều là giao điểm của 3 đường trung tuyến và cũng là đường cao, trung trực và phân giác trong.
Hình chóp tứ giác đều là gì?
*Định nghĩa:
Hình chóp tứ giác đều là hình chóp có đáy là hình vuông vắn, những mặt bên là những tam giác cân đối nhau có chung đỉnh
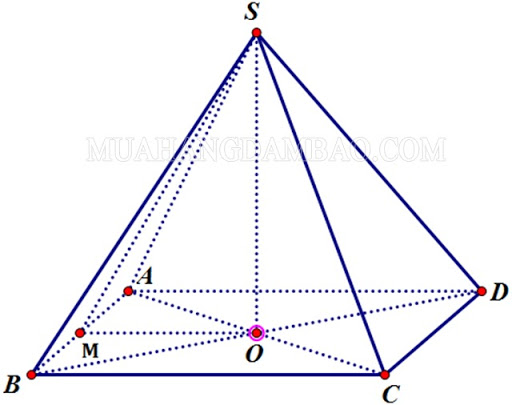
Hình chóp tứ giác đều
*Tính chất
Hình chóp có đáy là hình vuôngCác cạnh bên bằng nhauTất cả những mặt bên là những tam giác cân đối nhauChân đường cao trùng với tâm mặt đáy (tâm đáy là giao điểm của 2 đường chéo)Tất cả những góc tạo bởi cạnh bên và mặt đáy bằng nhauHình chóp tứ giác có 8 cạnh
Hình chóp cụt đều là gì?
*Định nghĩa:
Hình chóp cụt đều là hình chóp đều bị cắt bởi mặt phẳng song song với đáy. Phần hình chóp nằm giữa mặt phẳng đó và mặt phẳng đáy của hình chóp gọi là hình chóp cụt đều
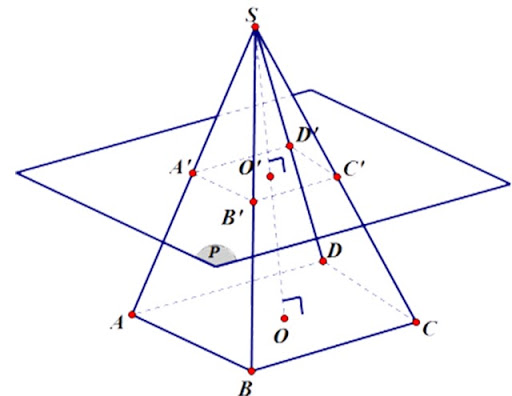
Hình chóp cụt đều
*Tính chất:
Mỗi mặt bên của hình chóp cụt đều là một hình thang cân
Công thức tính chu vi, diện tích s quy hoạnh, thể tích hình chóp
Công thức tính chu vi hình chóp (Áp dụng cho hình chóp tam giác, hình chóp tứ giác)
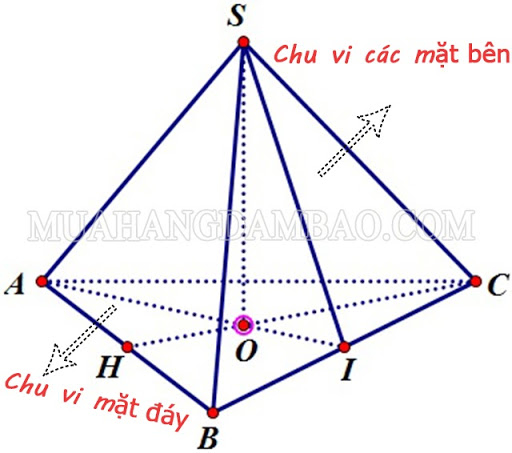
Công thức tính chu vi hình chóp
Chu vi hình chóp bằng tổng chu vi mặt đáy và những mặt bên
Công thức:
P = Pđáy + Pcác mặt bên
Trong số đó
Pđáy là chu vi mặt đáy
Pcác mặt bên là chu vi những mặt bên
Công thức tính diện tích s quy hoạnh hình chóp đều (Áp dụng cho hình chóp tam giác, hình chóp tứ giác)
Diện tích hình chóp gồm diện tích s quy hoạnh xung quanh và diện tích s quy hoạnh toàn phần.
Diện tích xung quanh
Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn
Công thức
Sxq = p.d

Diện tích xung quanh của hình chóp đều
Trong số đó:
p là nửa chu vi đáyd là trung đoạn của hình chóp. Trung đoạn là đường cao xuất phát từ đỉnh xuống trung điểm của một cạnh.
Xem thêm: Giải Phương Trình Sinx Sin3X = 0 ; Cosx + Cos2X + Cos3X = 0, Hỏi Đáp 24/7
Diện tích toàn phần của hình chóp:
Diện tích toàn phần của hình chóp bằng tổng diện tích s quy hoạnh xung quanh và diện tích s quy hoạnh đáy
Stp = Sxq + Sđáy
Như vậy, muốn tính được diện tích s quy hoạnh xung quanh và toàn phần của hình chóp bạn nên phải tính được độ dài trung đoạn và chu vi, diện tích s quy hoạnh đáy.
Thể tích hình chóp (Áp dụng cho hình chóp tam giác, hình chóp tứ giác)
Công thức
V=1/3S.h
Trong số đó:
S là diện tích s quy hoạnh đáy, h là độ cao
Thể tích hình chóp cụt 4 cạnh
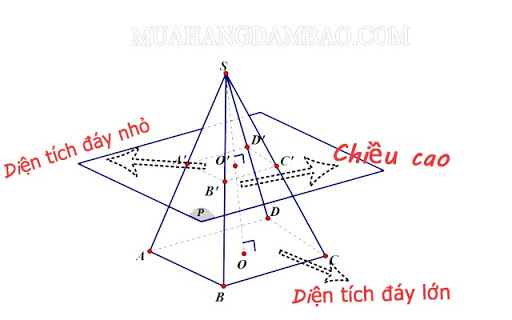
Thể tích hình chóp cụt 4 cạnh
Công thức:
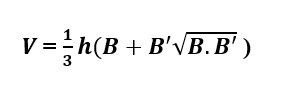
Trong số đó:
B’ và B lần lượt là diện tích s quy hoạnh của đáy nhỏ và đáy lớn của hình chóp cụt đều.h là độ cao (khoảng chừng cách giữa hai mặt đáy).
Phân biệt những hình chóp
Đáy Mặt bên Số cạnh đáy Số cạnh Số mặt Hình chóp tam giác đều Tam giác đều Tam giác đều 3 6 4 Hình chóp tứ giác đều Hình vuông Tam giác cân 4 8 5 Hình chóp ngũ giác đều Ngũ giác đều Tam giác cân 5 10 6 Hình chóp lục giác đều Lục giác đều Tam giác cân 6 12 7Dạng bài tập về hình chóp
Xác định quan hệ Một trong những yếu tố cạnh và mặt phẳng trong hình chóp đều, hình chóp cụt đều.
Xem thêm: Bài Tập Thì Hiện Tại Tiếp Diễn Cho Học Sinh Tiểu Học, Bài Tập Tiếng Anh Lớp 5 Thì Hiện Tại Tiếp Diễn
Sử dụng quan hệ song song và vuông góc Một trong những đường thẳng và mặt phẳng.Sử dụng những kiến thức và kỹ năng về hình chóp đều
Bài tập ví dụ:
Bài 1: Cho hình chóp SABC có SA vuông góc với mặt phẳng (ABC) và đáy ABC là tam giác vuông tại B, AB = a, SA = a. Lấy điểm H là hình chiếu của A trên cạnh SB. Khoảng cách giữa AH và BC bằng?

Đáp án:
Ta có BC⊥AB VÀ BC⊥SA→BC⊥(SAB)→BC⊥HB
Mà AH⊥HB→HB là đoạn vuông góc chung của AH và BC→d(AH,BC)=HB
Tam giác SAB vuông cân tại A có SA=SB=a, AH⊥SC
→

Bài 2: Cho hình chóp S ABCD là chóp tứ giác đều có những mặt bên là những tam giác đều, AB=8m, O là trung điểm của AC. Hình chóp S ABCD có mấy cạnh? Độ dài SO là bao nhiêu?
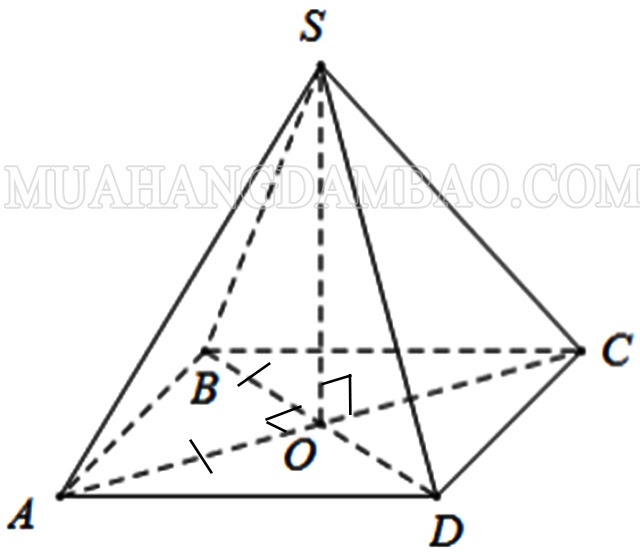
Đáp án:
Hình chóp S ABCD là hình chóp tứ giác nên có 8 cạnh
Hình chóp S ABCD đều nên đáy ABCD là hình vuông vắn ΔOAB vuông cân tại O
Áp dụng định lí Py-ta-go vào tam giác vuông ΔOAB có
AB2 = OB2+ OB2→ AB2 = 2OA2
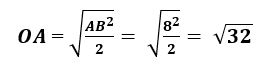
Hình chóp có những mặt bên là tam giác đều nên ΔSAB là tam giác đều. Do đó, SA = AB = 8m
Ta có SO⊥OA nên SOA vuông tại O
Áp dụng định lí Py-ta-go vào tam giác vuông SOA ta có:
SB2 = OS2+ OA2
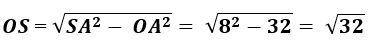
Mong rằng thông qua bài tổng hợp kiến thức và kỹ năng về hình chóp trên đây, những bạn đã hiểu và ghi nhớ được những công thức tính chu vi, diện tích s quy hoạnh, thể tích hình chóp và phân biệt được nhiều chủng quy mô chóp với nhau. Chúc những bạn có những giờ học hăng say và có ích.
Xem thêm nội dung bài viết thuộc phân mục: Diện tích
Tải thêm tài liệu liên quan đến nội dung bài viết Cách tính diện tích s quy hoạnh xung quanh hình chóp đều Mẹo Hay Cách
Post a Comment