Mẹo Khoảng cách giữa 2 đường thẳng Toán 10

Mẹo Hướng dẫn Khoảng cách giữa 2 đường thẳng Toán 10 2022

Lê Thùy Chi đang tìm kiếm từ khóa Khoảng cách giữa 2 đường thẳng Toán 10 được Cập Nhật vào lúc : 2022-09-08 17:02:02 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi tham khảo Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.

39

00:27:49 Bài 1: Tọa độ của vectơ trong không khí

40

00:40:44 Bài 2: Tọa độ của điểm trong không khí

45

00:18:23 Bài 7: Ứng dụng tích được bố trí theo hướng tính diện tích s quy hoạnh

46

00:22:03 Bài 8: Ứng dụng tích được bố trí theo hướng tính thể tích

48

00:32:07 Bài 9: Bài toán viết phương trình mặt phẳng

51

00:19:42 Bài 12: Bài toán góc Một trong những mặt phẳng

53

Kiểm tra: Đề thi online phần Mặt phẳng

57

00:14:57 Bài 17: Góc giữa hai tuyến đường thẳng

58

00:15:13 Bài 18: Góc giữa đường thẳng và mặt phẳng

60

Kiểm tra: Đề thi online phần Đường thẳng

61

00:19:21 Bài 20: Bài toán viết phương trình mặt cầu

65

Kiểm tra: Đề thi online phần Mặt cầu

66

00:37:14 Bài 24: Ôn tập, nâng cao

Tìm khoảng chừng cách giữa hai tuyến đường thẳng song song Toán học lớp 10 với đầy đủ lý thuyết, phương pháp giải và bài tập có lời giải cho tiết sẽ giúp học viên nắm được Tìm khoảng chừng cách giữa hai tuyến đường thẳng song song
 

  Tải tài liệu

« Trang trước Trang sau »

A. Phương pháp giải

d( d; d’) = d( A; d’) trong đó A là một điểm thuộc đường thẳng d.

⇒ Để tính khoảng chừng cách hai tuyến đường thẳng song song ta cần:

+ Đưa phương trình hai tuyến đường thẳng về dạng tổng quát.

+ Lấy một điểm A bất kì thuộc đường thẳng d.

+ Tính khoảng chừng cách từ điểm A đến đường thẳng d’ .

+ Kết luận: d( d; d’) = d( A; d’) .



B. Ví dụ minh họa

Ví dụ 1: Cho tam giác ABC có B( 1; -2) và C( 0; 1). Điểm A thuộc đường thẳng
d: 3x+ y= 0 .Tính diện tích s quy hoạnh tam giác ABC.

A. 1    B. 3    C. 0,5    D. 2

Lời giải

+ Phương trình đường thẳng BC:



⇒ Phương trình BC: 3(x - 1) + 1(y + 2) = 0 hay 3x + y - 1 = 0 .

+ ta có; BC =  = √10

+ Xét vị trí tương đối giữa đường thẳng d và BC:

Ta có:  ⇒ d // BC.

Mà điểm A thuộc d nên d( A; BC) = d( d; BC) . (1)

+ Ta tính khoảng chừng cách hai tuyến đường thẳng d và BC.

Lấy điểm O(0; 0) thuộc d.

⇒ d(d; BC) = d(O;BC) =  =  ( 2)

Từ ( 1) và ( 2) suy ra d( A; BC) =  .

+ Diện tích tam giác ABC là S =  d( A,BC).BC =  . .√10 = 0, 5

Chọn C.

Ví dụ 2. Tính khoảng chừng cách giữa hai tuyến đường thẳng d: 7x + y - 3 = 0 và ∆:  .

A.     B. 15    C. 9    D. 

Lời giải

+ Ta đưa đường thẳng ∆ về dạng tổng quát:

∆: 

⇒ Phương trình ∆: 7( x + 2) + 1( y - 2) = 0 hay 7x + y + 12 = 0

Ta có:  nên d // ∆

⇒ d(d;Δ) = d(A;d) = 

Chọn A.

Ví dụ 3. Tập hợp những điểm cách đường thẳng ∆: 3x - 4y + 2 = 0 một khoảng chừng bằng 2 là hai tuyến đường thẳng có phương trình nào sau đây?

A. 3x - 4y + 8 = 0 hoặc 3x - 4y + 12 = 0.    B. 3x - 4y - 8 = 0 hoặc 3x - 4y + 12 = 0.

C. 3x - 4y - 8 = 0 hoặc 3x - 4y - 12 = 0.    D. 3x - 4y + 8 = 0 hoặc 3x - 4y - 12 = 0.

Lời giải

Gọi điểm M (x ; y) là vấn đề cách đường thẳng ∆ một khoảng chừng bằng 2. Suy ra :

d(M(x; y); Δ) = 2 ⇔  = 2

|3x - 4y + 2| = 10 ⇒ 

Vậy tập hợp những điểm cách ∆ một khoảng chừng bằng 2 là hai tuyến đường thẳng :

3x - 4y + 12 = 0 và 3x - 4y - 8 = 0

Chọn B.

Ví dụ 4. Trong mặt phẳng với hệ tọa độ Oxy, cho hai tuyến đường thẳng d1: 5x + 3y - 3 = 0 và d2: 5x + 3y + 7 = 0 song song nhau. Đường thẳng d vừa song song và cách đều với d1; d2 là:

A. 5x + 3y - 2 = 0    B. 5x + 3y + 4 = 0    C. 5x + 3y + 2 = 0    D. 5x + 3y - 4 = 0

Lời giải

Lấy điểm M ( x; y) thuộc đường thẳng d. Suy ra:

d(M(x; y); d1)=d(M(x; y); d2) ⇔ 

⇔ 

Đường thẳng d: 5x + 3y + 2 song song với hai tuyến đường thẳng d1 và d2.

Vậy đường thẳng d thỏa mãn là: 5x + 3y + 2 = 0

Chọn C.

Ví dụ 5: Cho đường thẳng d:  và đường thẳng ∆:  . Tính khoảng chừng cách hai tuyến đường thẳng này.

A. 1    B. 0.    C. 2    D. 3

Lời giải

+ Đường thẳng d: 

⇒ Phương trình d: 3(x - 2) – 2(y + 1) = 0 hay 3x - 2y - 8 = 0

+ Đường thẳng ∆: 

⇒ Phương trình ∆: 3(x - 0) – 2(y + 4) = 0 hay 3x - 2y - 8 = 0

⇒ hai tuyến đường thẳng này trùng nhau nên khoảng chừng cách hai tuyến đường thẳng này là 0.

Chọn B.

Ví dụ 6: Cho hai tuyến đường thẳng d: x + y - 2 = 0 và đường thẳng ∆:  . Viết phương trình đường thẳng d’// d sao cho khoảng chừng cách hai tuyến đường thẳng d’ và ∆ là √2.

A. x + y - 1 = 0    B. x + y + 1= 0    C. x + y - 3 = 0    D. Cả B và C đúng.

Lời giải

+ Do đường thẳng d’// d nên đường thẳng d có dạng (d’) : x + y + c = 0( c ≠ -2)

+ Đường thẳng ∆: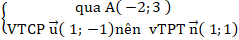 

⇒ Phương trình ∆: 1(x + 2) + 1(y - 3) = 0 hay x + y - 1 = 0.

+ Lấy điểm M ( 1; 0) thuộc ∆.

Để khoảng chừng cách hai tuyến đường thẳng d’ và ∆ bằng 2 khi và chỉ khi:

d( d’; ∆) = d( M; d’) = 2

⇔  = √2 ⇔ |1 + c| = 2

⇔

Vậy có hai tuyến đường thẳng thỏa mãn là : x + y + 1 = 0 và x + y - 3 = 0

Chọn D.

Ví dụ 7: Khoảng cách giữa hai tuyến đường thẳng ∆: 6x - 8y - 101 = 0 và d: 3x - 4y = 0 là:

A. 10, 1    B. 1,01    C. 12    D. √101 .

Hướng dẫn giải

+ Ta có: 

⇒ Hai đường thẳng đã cho song song với nhau: d // ∆.

+ Lấy điểm O( 0;0) thuộc đường thẳng d.

+ Do hai tuyến đường thẳng d và ∆ song song với nhau nên

d(∆; d) = d ( O; ∆) =  = 10,1

Chọn A.

C. Bài tập vận dụng

Câu 1: Cho đường thẳng d: 3x - 4y + 2 = 0. Có đường thẳng a và b cùng song song với d và cách d một khoảng chừng bằng 1. Hai đường thẳng đó có phương trình là:

A. 3x + 4y - 1 = 0 ; 3x + 4y + 5 = 0    B. 3x - 4y + 7 = 0 ; 3x - 4y - 3 = 0

C. 3x + 4y - 3 = 0 ; 3x + 4y + 7 = 0    D. 3x - 4y + 6 = 0; 3x - 4y - 4 = 0

Câu 2: Cho đường thẳng d: x - 2y + 2 = 0 . Phương trình những đường thẳng song song với d và cách d một đoạn bằng √5 là

A. x - 2y - 3 = 0; x - 2y + 7 = 0    B. x - 2y + 3 = 0 và x - 2y + 7 = 0

C. x - 2y - 3 = 0; x - 2y - 7 = 0    D. x - 2y + 3 = 0; x - 2y - 7 = 0 .

Câu 3: Cho đường thẳng d: 3x + 4y + 1 = 0. Có 2 đường thẳng d1 và d2 cùng song song với d và cách d một khoảng chừng bằng 1. Hai đường thẳng đó có phương trình là:

A. 3x + 4y - 7 = 0; 3x - 4y + 3 = 0.    B. 3x - 4y + 7 = 0; 3x - 4y - 3 = 0

C. 3x + 4y + 4 = 0; 3x + 4y + 3 = 0.    D. 3x + 4y - 4 = 0; 3x + 4y + 6 = 0 .

Câu 4: Khoảng cách giữa 2 đường thẳng (a): 7x + y - 3 = 0 và (b): 7x + y + 12 = 0 là

A.     B. 9.    C.     D. 15.

Câu 5: Cho hai tuyến đường thẳng d: x + y - 4 = 0 và đường thẳng ∆:  . Tính khoảng chừng cách giữa hai tuyến đường thẳng này?

A. 1    B. 2    C. √2    D. Đáp án khác

Câu 6: Cho đường thẳng d: 2x - 3y + 6 = 0 và đường thẳng ∆: 4x - 6y + 20 = 0. Viết phương trình đường thẳng d’ // d sao cho khoảng chừng cách hai tuyến đường thẳng d’ và ∆ là √13

A. 2x - 3y + 23 = 0    B. 2x - 3y - 3 = 0.

C. 2x - 3y – 8 = 0 và 2x - 3y = 0    D. Cả A và B đúng

Câu 7: Cho tam giác ABC có B( - 2; 1) và C( 2; 0). Điểm A thuộc đường thẳng
d: x+ 4y- 10= 0 .Tính diện tích s quy hoạnh tam giác ABC.

A. 1    B. 3    C. 0,5    D. 

Bài viết liên quan

  Tải tài liệu

« Trang trước Trang sau »

Tải thêm tài liệu liên quan đến nội dung bài viết Khoảng cách giữa 2 đường thẳng Toán 10

Video Khoảng cách giữa 2 đường thẳng Toán 10 ?

Bạn vừa tham khảo tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Review Khoảng cách giữa 2 đường thẳng Toán 10 tiên tiến nhất

Chia Sẻ Link Download Khoảng cách giữa 2 đường thẳng Toán 10 miễn phí

Bạn đang tìm một số trong những Share Link Down Khoảng cách giữa 2 đường thẳng Toán 10 Free.

Hỏi đáp thắc mắc về Khoảng cách giữa 2 đường thẳng Toán 10

Nếu sau khi đọc nội dung bài viết Khoảng cách giữa 2 đường thẳng Toán 10 vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Ad lý giải và hướng dẫn lại nha #Khoảng #cách #giữa #đường #thẳng #Toán