Review Phương trình biểu diễn năng lượng bức xạ của vật
Mẹo về Phương trình màn biểu diễn năng lượng bức xạ của vật 2022
Bùi Đàm Mai Phương đang tìm kiếm từ khóa Phương trình màn biểu diễn năng lượng bức xạ của vật được Update vào lúc : 2022-08-05 10:26:02 . Với phương châm chia sẻ Kinh Nghiệm về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha.Thuyết động học phân tử cho biết thêm thêm bản chất của nhiệt đó đó là sự việc hoạt động và sinh hoạt giải trí hỗn loạn của những phân tử, đánh đổ hoàn toàn những quan điểm về chất nhiệt trước đó. Nó lý giải thỏa đáng mọi hiện tượng kỳ lạ và tính chất nhiệt của những chất. Từ phương trình cơ bản (7.1), ta tìm được phương trình trạng thái khí lí tưởng, kiểm nghiệm lại những định luật thực nghiệm về chất khí trước đó.
Nội dung chính- 1. Phương trình trạng thái khí lí tưởng 2. Các định luật thực nghiệm về chất khíTài liệu tham khảo[sửa]
1. Phương trình trạng thái khí lí tưởng
Trạng thái của một hệ vật lý được mô tả bởi những thông số – gọi là thông số trạng thái. Thông số nào đặc trưng cho tính chất vi mô của hệ thì ta gọi đó là thông số vi mô; thông số nào đặc trưng cho tính chất vĩ mô của hệ thì ta gọi đó là thông số vĩ mô.
Trạng thái của một khối khí lí tưởng hoàn toàn có thể được mô tả bởi những thông số vĩ mô: nhiệt độ T, áp suất p và thể tích V. Phương trình diễn tả quan hệ Một trong những thông số đó, được gọi là phương trình trạng thái lí tưởng. Ta hoàn toàn có thể tìm được quan hệ này từ phương trình cơ bản của thuyết động học phân tử (7.1).
Thật vậy: Nếu gọi n là nồng độ (tỷ lệ) phân tử khí thì số phân tử khí chứa trong thể tích V là: ( N = nV ).
Từ (7.4), suy ra: ( p.V=nkT.V=NkT=fracNN_AN_AkT ), với NA là số phân tử chứa trong một mol khí ( ( N_A=6,02.10^23text mol^-1 ) do nhà Bác học Avogadro xác lập nên được gọi là số Avogadro); ( fracNN_A=fracmmu ) = số mol khí.
Vậy: ( pV=fracmmu RT ) (7.6)
trong đó, R là hằng số khí lí tưởng:
(R=k.N_A=1,38.10^-23.6,02.10^-23=8,31text left( J.mol^-1.K^-1 right))(=0,082text left( atm.lit.mol^-1.K^-1 right)=0,084text left( .lit.mol^-1.K^-1 right))
Phương trình (7.6) được gọi là phương trình Mendeleev – Clapeyron. Đó chính phương trình trạng thái của một khối khí lí tưởng bất kì.
Đối với một khối khí xác định (m = const), ta có: ( fracpVT=const ) (7.7)
Vậy, với một khối khí xác định, khi biến hóa từ trạng thái (1) sang trạng thái (2) thì: ( fracp_1V_1T_1=fracp_2V_2T_2 ) (7.8)
(7.7) và (7.8) là những phương trình trạng thái của một khối khí lí tưởng xác định.
2. Các định luật thực nghiệm về chất khí
Từ (7.7) ta hoàn toàn có thể tìm lại những định luật thực nghiệm về chất khí.
a) Định luật Boyle – Mariotte
Khi ( T = const ), từ (7.7), suy ra: ( pV = const ) (7.9)
Hay p1V1 = p2V2 (7.9a)
Vậy, ở nhiệt độ nhất định, áp suất và thể tích của một khối khí xác định tỉ lệ nghịch với nhau.
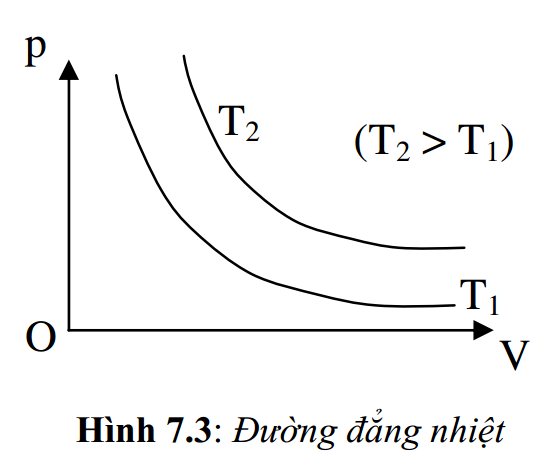
Đường màn biểu diễn áp suất p biến thiên theo thể tích V khi nhiệt độ không đổi được gọi là đường đẳng nhiệt. Đường đẳng nhiệt là một đường cong Hyperbol. Với những nhiệt độ rất khác nhau thì đường thẳng nhiệt cũng rất khác nhau. Đường nằm trên có nhiệt độ cao hơn đường nằm dưới (T2 > T1) (hình 7.3).
b) Định luật Gay Lussac
Khi ( p = const ), từ (6.7) suy ra: ( fracVT=const ) hay ( fracV_1T_1=fracV_2T_2 ) (7.10)
Vậy, ở áp suất nhất định, thể tích và nhiệt độ tuyệt đối của một khối khí xác định tỉ lệ thuận với nhau.
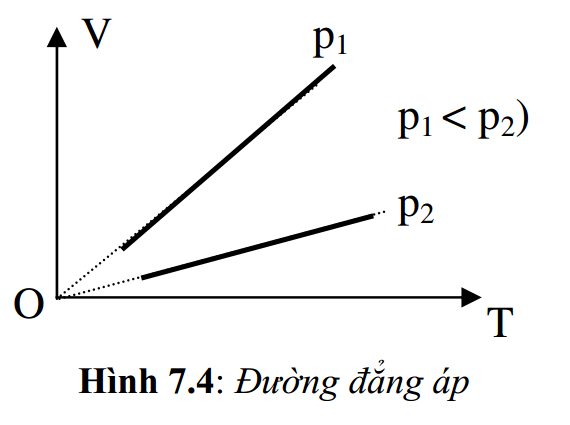
Đường màn biểu diễn thể tích V biến thiên theo nhiệt độ T khi áp suất không đổi, được gọi là đường đẳng áp. Đường đẳng áp là một đường thẳng có phương đi qua gốc tọa độ (hình 7.4). Áp suất càng thấp đường màn biểu diễn càng dốc.
c) Định luật Charles
khi V = const, tương tự, ta cũng luôn có thể có: ( fracpT=const ) hay ( fracp_1T_1=fracp_2T_2 ) (7.11)
Vậy, ở thể tích nhất định, áp suất và nhiệt độ tuyệt đối của một khối khí xác định tỉ lệ thuận với nhiệt nhau.
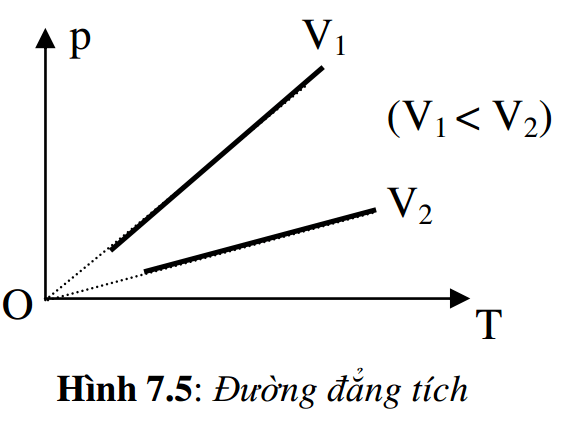
Đường màn biểu diễn áp suất p biến thiên theo nhiệt độ T khi thể tích không đổi, được gọi là đường đẳng tích. Đường đẳng tích là một đường thẳng có phương qua gốc tọa độ và có độ dốc càng lớn khi thể tích càng nhỏ.
d) Định luật Dalton
Xét một bình kín chứa một hỗn hợp gồm m chất khí rất khác nhau. Gọi n1, n2, …., nm là nồng độ tương ứng của những khí thành phần thì nồng độ của hỗn hợp khí đó là n = n1 + n2 + … + nm.
Theo (7.4), ta có: ( p=nkT=left( n_1+n_2+n_3+…+n_m right)kT )
Hay ( p=n_1kT+n_2kT+n_3kT+…+n_mkT=p_1+p_2+…+p_m ) (7.12)
Vậy, áp suất của một hỗn hợp khí bằng tổng những áp suất riêng phần của những khí thành phần tạo nên.
Giả thuyết Planck về lượng tử năng lượng là giả thuyết tân tiến về tính chất gián đoạn (lượng tử) của năng lượng bức xạ.
Nhà Vật lý M. Planck (Đức) đưa ra năm 1900.
Khủng hoảng tử ngoại: vào thời điểm cuối thế kỷ XIX, những nhà Vật lý gặp trở ngại vất vả lớn trong việc lý giải dạng của đồ thị màn biểu diễn sự phụ thuộc của năng suất phát xạ đơn sắc của vật đen tuyệt đối vào bước sóng ánh sáng.
Dựa vào lý thuyết phát xạ cổ xưa, người ta thấy rằng năng suất phát xạ đơn sắc của vật đen tuyệt đối phải tỷ lệ với bình phương của tần số (tức là tỷ lệ nghịch với bình phương của bước sóng). Như vậy, khi λ → 0 displaystyle lambda rightarrow 0
thì năng suất phát xạ đơn sắc ρ ( λ , T ) → ∞ displaystyle rho (lambda ,T)rightarrow infty
. Điều này hoàn toàn xích míc với kết quả thực nghiệm. Người ta gọi sự bất lực của lý thuyết phát xạ cổ xưa trong trường hợp này là sự việc khủng hoảng rủi ro cục bộ tử ngoại.
Giả thuyết (định luật) Planck: Planck nhận định rằng nguyên nhân cơ bản dẫn đến sự thất bại của lý thuyết phát xạ cổ xưa trong sự lý giải những kết quả thực nghiệm về sự bức xạ của vật đen tuyệt đối, là quan niệm sai lầm về độ lớn của năng lượng mà một nguyên tử hoặc phân tử hoàn toàn có thể trao đổi với bên phía ngoài, mỗi lần phát xạ hay hấp thụ bức xạ.
Theo Giả thuyết Planck về lượng tử năng lượng, lượng năng lượng mà một nguyên tử hay phân tử trao đổi mỗi lần phát xạ hay hấp thụ bức xạ có mức giá trị hoàn toàn xác định, bằng
ε = h f , displaystyle varepsilon =hf,
(1)
ε displaystyle varepsilon
gọi là lượng tử năng lượng, f displaystyle f
là tần số của bức xạ được phát ra hay bị hấp thụ và ℎ là một hằng số. Sau này người ta đặt tên hằng số đó là hằng số Planck và đã xác định được đúng chuẩn giá trị của nó:
h = 6 , 625.10 − 34 J . s displaystyle h=6,625.10^-34J.s
(2)
Công thức Planck về bức xạ nhiệt: xuất phát từ Giả thuyết Planck về lượng tử năng lượng nói trên, Planck đã thiết lập được công thức màn biểu diễn sự phụ thuộc của năng suất phát xạ đơn sắc của vật đen tuyệt đối vào tần số f displaystyle f
và nhiệt độ ρ ( f , T ) displaystyle rho (f,T)
(hoặc vào bước sóng và nhiệt độ ρ ( λ , T ) displaystyle rho (lambda ,T)
. Công thức này được gọi là công thức Planck về bức xạ nhiệt, hay còn gọi là định luật bức xạ Planck, có dạng sau:
ρ ( f , T ) = ( 2 π f 2 c 2 ) h f ( e x p h f / k T − 1 ) , displaystyle rho (f,T)=left(frac 2pi f^2c^2right)frac hf(exphf/kT-1),
(3)
hay
ρ ( λ , T ) = 2 π h c 2 λ 5 1 ( e x p h c / λ k T − 1 ) , displaystyle rho (lambda ,T)=frac 2pi hc^2lambda ^5frac 1(exphc/lambda kT-1),
(4)
Hệ quả của công thức Planck về bức xạ nhiệt: từ công thức (3) và (4), ta hoàn toàn có thể suy ra những định luật về bức xạ nhiệt của vật đen tuyệt đối. Độ trưng năng lượng toàn phần RT của vật đen tuyệt đối là
R T = ∫ 0 ∞ ρ ( f , T ) d f = σ T 4 displaystyle R_T=int limits _0^infty rho (f,T)df=sigma T^4
(5)
trong đó σ = 5 , 67.10 − 8 W / m 2 . K 4 displaystyle sigma =5,67.10^-8W/m^2.K^4
. Đó là định luật Stefan-Boltzmann.
Tính đạo hàm của ρ ( λ , T ) displaystyle rho (lambda ,T)
theo λ displaystyle lambda
, ta thấy đạo hàm này triệt tiêu khi λ = λ m a x displaystyle lambda =lambda _max
, ứng với giá trị cực lớn của năng suất phát xạ đơn sắc của vật đen tuyệt đối:
λ = b T , displaystyle lambda =frac bT,
(6)
với b = 2 , 898.10 − 3 m . K displaystyle b=2,898.10^-3m.K
. Đó đó đó là định luật dịch chuyển Wien.
Tài liệu tham khảo[sửa]
J.P. Pérez, Thermodynamique, Fondements et applications, Masson, Paris, 1997. Oxford Dictionary of Physics, Alan Isaacs (Ed), Oxford University Press, Tp New York, 2000. D. Haliday, R. Resnick, J. Walker, Fundamentals of Physics, John Wiley Inc., Tp New York, 2014.
Post a Comment