Mẹo Tính thể tích v của phần vật thể giới hạn bởi hai mặt phẳng x=1 và x=4
Mẹo Hướng dẫn Tính thể tích v của phần vật thể số lượng giới hạn bởi hai mặt phẳng x=1 và x=4 Mới Nhất
Hoàng Thị Bích Ngọc đang tìm kiếm từ khóa Tính thể tích v của phần vật thể số lượng giới hạn bởi hai mặt phẳng x=1 và x=4 được Cập Nhật vào lúc : 2022-08-05 01:44:01 . Với phương châm chia sẻ Bí kíp về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha.
Các thắc mắc tương tự
Tính thể tích V của phần vật thể số lượng giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và 3 x 2 - 2
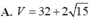
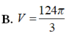
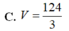
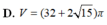
Tính thể tích Vcủa vật thể số lượng giới hạn bởi hai mặt phẳng x=0 và x=4, biết rằng khi cắt bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x (0 < x < 4) thì được thiết diện là nửa hình tròn trụ có bán kính R = x 4 - x .
A. 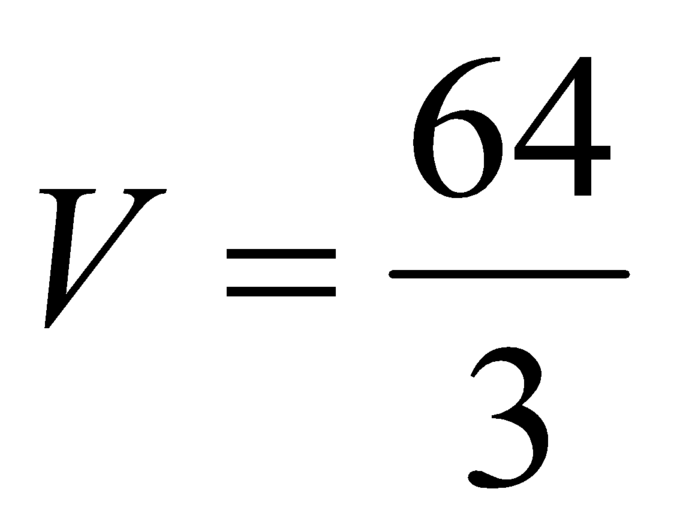 .
.
B.
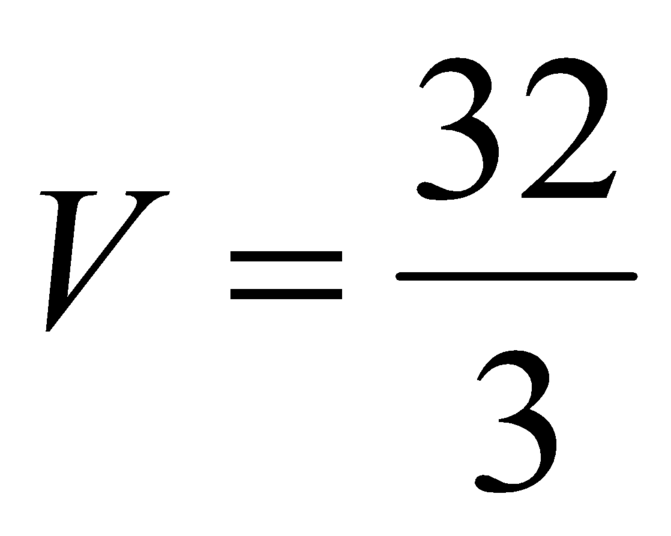 .
. C.
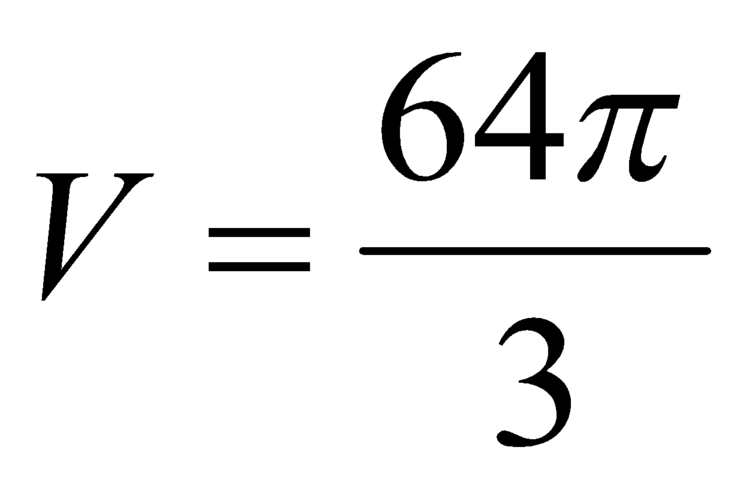 .
. D.
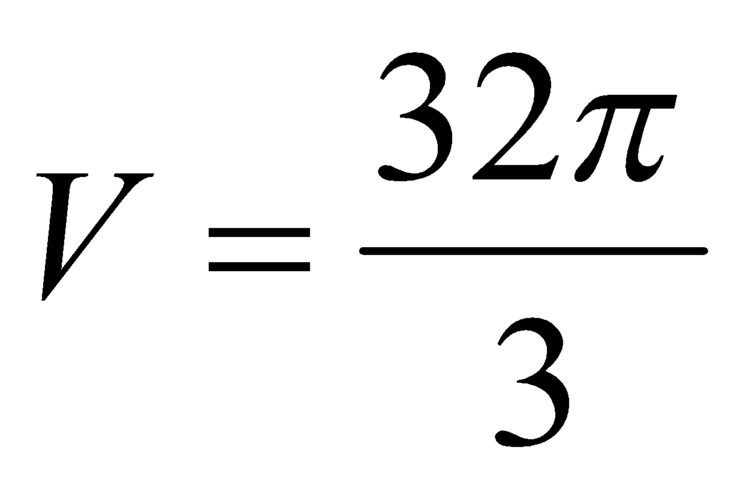 .
.
Cho phần vật thể (T) số lượng giới hạn bởi hai mặt phẳng có phương trình x=0 và x=2. Cắt phần vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x, ta được thiết diện là một tam giác đều có độ dài cạnh bằng x 2 - x . Tính thể tích V của phần vật thể (T).
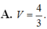
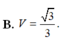
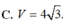
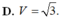
Tính thể tích của phần vật thể số lượng giới hạn bởi hai mặt phẳng x = 0 và x = 3, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 3 là một hình chữ nhật có hai kích thước là x và 2 9 - x 2 .
A. 16
B. 17
C. 19
D. 18
Thể tích phần vật thể số lượng giới hạn bởi hai mặt phẳng x = 0 và x = 3 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(0 ≤ x ≤ 3) là một hình chữ nhật có hai kích thước là x và 2 ( 9 - x 2 )
A. 6 3
B. 18
C. 2 3 3
D. 3 3 3
Cho vật thể số lượng giới hạn bởi hai mặt phẳng x = 0 ; x = π 2 , biết rằng thiết diện của vật thể khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 0 ≤ x ≤ π 2 ) là một hình tròn trụ có bán kính R = cos x Thể tích của vật thể đó là
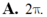
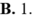
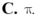
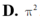
Tính thể tích vật thể số lượng giới hạn bởi hai mặt phẳng x = 0 , x = π . Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác vuông cân có cạnh huyền bằng sin x + 2 .
A. 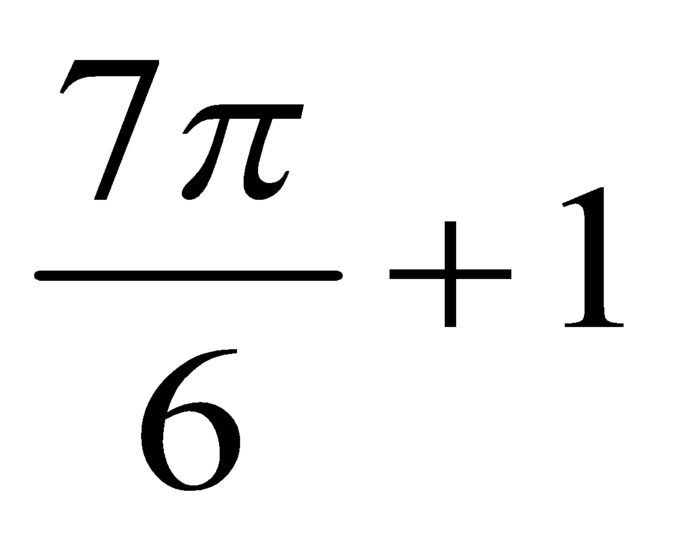
B.
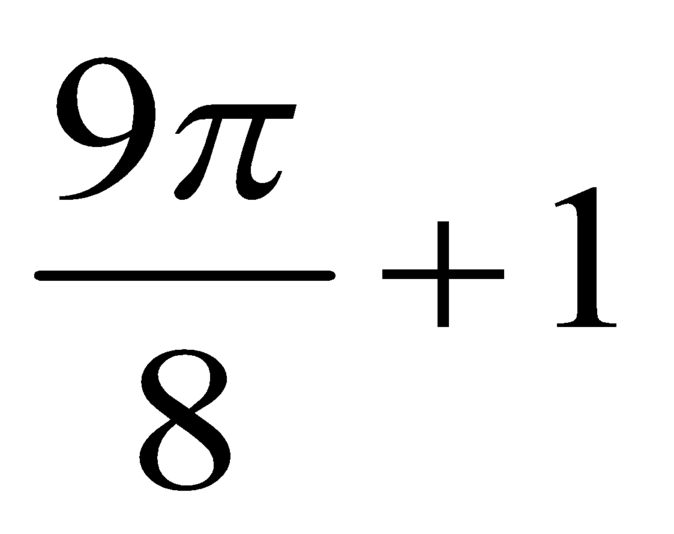
C.
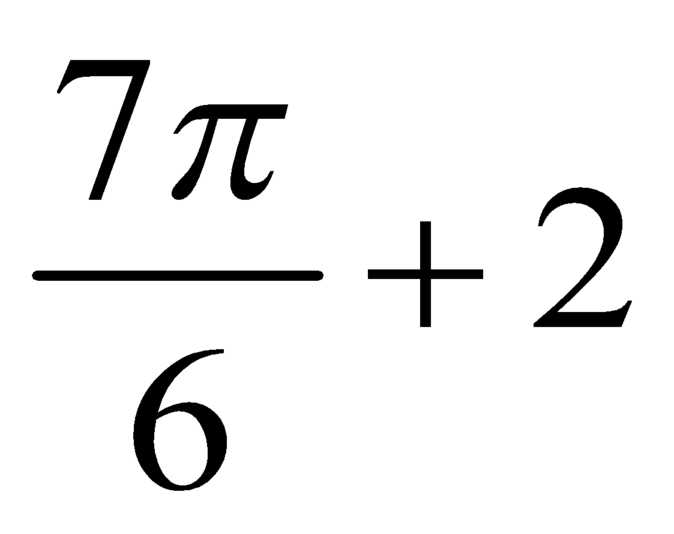
D.
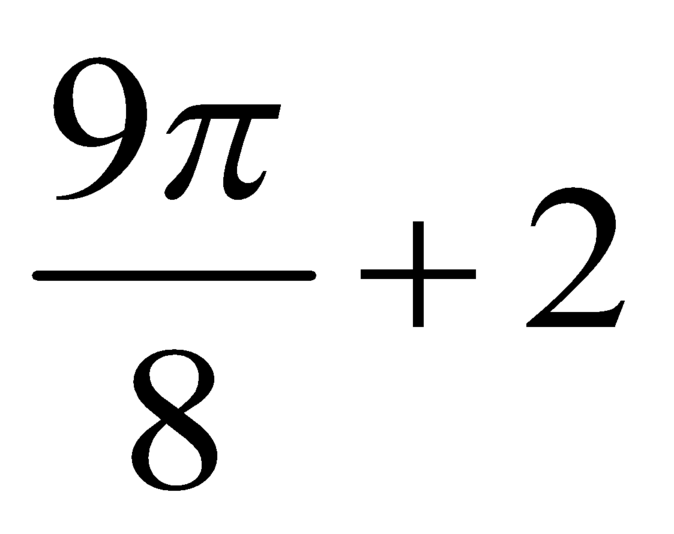
Giới thiệu về cuốn sách này
Page 2Giới thiệu về cuốn sách này
Tính thể tích V của phần vật thể số lượng giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(left( 1 le x le 3 right)) thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và (sqrt 3x^2 - 2 ).
A.
(V = 32 + 2sqrt 15 )
B.
(V = 124pi over 3)
C.
D.
(V = left( 32 + 2sqrt 15 right)pi )
Cho hình phẳng số lượng giới hạn bởi $D = left y = tan x;,,y = 0;,,x = 0;,,x = dfracpi 3 right.$ Thể tích vật tròn xoay khi $D$ quay quanh trục $Ox$ là $V = pi left( a - dfracpi b right),$ với $a,,,b in R.$ Tính $T = a^2 + 2b.$
Gọi (left( D_1 right)) là hình phẳng số lượng giới hạn bởi những đường (y = 2sqrt x ,,,y = 0) và (x = 2022,) (left( D_2 right)) là hình phẳng số lượng giới hạn bởi những đường (y = sqrt 3 x,,,y = 0) và (x = 2022.) Gọi (V_1,,,V_2) lần lượt là thể tích khối tròn xoay tạo thành khi quay (left( D_1 right)) và (left( D_2 right)) xung quanh trục (Ox.) Tỉ số (dfracV_1V_2) bằng:
Bằng cách đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách Bảo mật của chúng tôi.
Tính thể tích V của phần vật thể số lượng giới hạn bởi hai mặt phẳng x=1và x=4, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x (1≤x≤4) thì được thiết diện là một hình lục giác đều có độ dài cạnh là 2x.
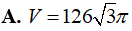
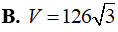
Đáp án đúng chuẩn
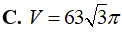
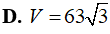
Xem lời giải

Post a Comment