Mẹo Hàm số f(x)=x^4 x+1 2 có bao nhiêu điểm cực trị
Thủ Thuật Hướng dẫn Hàm số f(x)=x^4 x+1 2 có bao nhiêu điểm cực trị Chi Tiết
Gan Feng Du đang tìm kiếm từ khóa Hàm số f(x)=x^4 x+1 2 có bao nhiêu điểm cực trị được Update vào lúc : 2022-08-19 02:02:03 . Với phương châm chia sẻ Kinh Nghiệm về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha.
Trong khoá học PRO X những em đã được tiếp cận cách xác định số điểm cực trị của hàm trị tuyệt đối nhờ vào cách suy đồ thị và bảng biến thiên. Ở nội dung bài viết này trình bày cho những em công thức tính nhanh:
Nội dung chính- Nhận xét: Đặc biệt với hàm số $f(x)=ax^3+bx^2+cx+d$ có hai điểm cực trị $x_1,x_2.$ Khi đó hàm số $y=left| f(x) right|$ có $n$ điểm cực trịVí dụ 1: Cho hàm số bậc ba $y=fleft( x right)$có đồ thị của hàm đạo hàm $f'left( x right)$ như hình vẽ và $fleft( b right)=1$.Số giá trị nguyên của $min left[ -5;5 right]$ để hàm số $gleft( x right)=left| f^2left( x right)+4fleft( x right)+m right|$ có đúng 5 điểm cực trị làVí dụ 2: Cho hàm số $f(x)$ có $f(0)=0$ và $f'(x)$ là đa thức bậc bốn có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số $g(x)=left| f(x^3)+x right|$ làTuyển tập Đề thi thử Toán THPT Quốc gia 2022 có lời giải chi tiếtVideo liên quan
Nội dung lý thuyết và ví dụ những bài toán trong nội dung bài viết này được trình bày tại khoá học PRO XMAX bạn đọc tham khảo thêm tại đây: https://www.vted/khoa-hoc/xem/khoa-pro-xmax-chinh-phuc-nhom-cau-hoi-van-dung-cao-2022-mon-toan-kh646448377.html
[embed]https://www.youtube.com/watch?v=9hNUrmY7hcQ[/embed]
[embed]https://www.youtube.com/watch?v=mSy3fAridH0[/embed]

Nhận xét:
Đặc biệt với hàm số $f(x)=ax^3+bx^2+cx+d$ có hai điểm cực trị $x_1,x_2.$ Khi đó hàm số $y=left| f(x) right|$ có $n$ điểm cực trị
Ví dụ 1: Cho hàm số bậc ba $y=fleft( x right)$có đồ thị của hàm đạo hàm $f'left( x right)$ như hình vẽ và $fleft( b right)=1$.
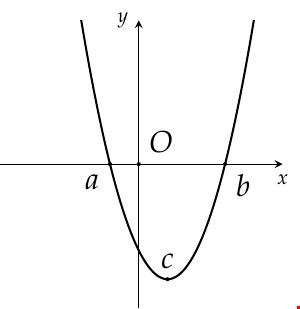
Số giá trị nguyên của $min left[ -5;5 right]$ để hàm số $gleft( x right)=left| f^2left( x right)+4fleft( x right)+m right|$ có đúng 5 điểm cực trị là
A. $8$.
B. $10$.
C. $9$.
D. $7$.
Lời giải rõ ràng. Ta có bảng biến thiên của hàm số $y=fleft( x right)$:
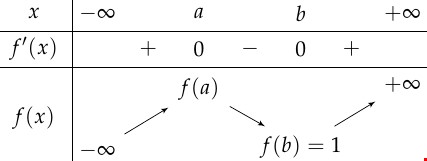
Xét hàm số $hleft( x right)=f^2left( x right)+4fleft( x right)+m$.
Ta có $h'left( x right)=2f'left( x right)fleft( x right)+4f'left( x right)=2f'left( x right)left[ fleft( x right)+2 right]$.
Khi đó $h'left( x right)=0Rightarrow 2f'left( x right)left[ fleft( x right)+2 right]=0Leftrightarrow left[ begingatheredhfill f'left( x right)=0 \ hfill fleft( x right)=-2 \ endgathered right.Leftrightarrow left[ begingatheredhfill x=a;,x=b \ hfill x=c,,left( c,,langle ,,a right) \ endgathered right.$.
Vậy $h'left( x right)=0$ có $3$ nghiệm phân biệt $Rightarrow $$hleft( x right)$có $3$ điểm cực trị.
Xét $hleft( x right)=0$$Leftrightarrow f^2left( x right)+4fleft( x right)=-m,,left( * right)$.
Để $gleft( x right)=left| hleft( x right) right|$có $5$ điểm cực trị khi và chỉ khi PT $left( * right)$có $2$ nghiệm đơn hoặc nghiệm bội lẻ phân biệt.
Xét hàm số $tleft( x right)=f^2left( x right)+4fleft( x right)$.
Ta có $t'left( x right)=2.fleft( x right).f'left( x right)+4f'left( x right)=2f'left( x right)left[ fleft( x right)+2 right]$.
Khi đó $t'left( x right)=0Leftrightarrow 2f'left( x right)left[ fleft( x right)+2 right]=0Leftrightarrow left[ begingatheredhfill f'left( x right)=0 \ hfill fleft( x right)=-2 \ endgathered right.$$Leftrightarrow left[ begingatheredhfill x=a;,x=b \ hfill x=c,,left( c,,langle ,,a right) \ endgathered right.$.
Ta có $tleft( c right)=f^2left( c right)+4fleft( c right)=left( -2 right)^2-8=-4.$ $tleft( b right)=f^2left( b right)+4fleft( b right)=5.$
Ta có bảng biến thiên của $tleft( x right)$:
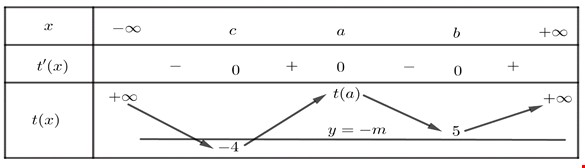
Từ YCBT $Leftrightarrow tleft( x right)=-m$ có hai nghiệm đơn hoặc nghiệm bội lẻ phân biệt
$Leftrightarrow left{ begingatheredhfill left[ begingatheredhfill -mge tleft( a right)>5 \ hfill -4<-mle 5 \ endgathered right. \ hfill -5le mle 5;,min mathbbZ \ endgathered right.Leftrightarrow left{ begingatheredhfill left[ begingatheredhfill mle -tleft( a right)<-5 \ hfill -4<-mle 5 \ endgathered right. \ hfill -5le mle 5, \ endgathered right.Leftrightarrow left{ begingatheredhfill -5le m<4 \ hfill min mathbbZ \ endgathered right.$
$Leftrightarrow min left -5;-4;-3;-2;-1;0;1;2;3 right.$ Vậy có $9$ giá trị nguyên của $m$ thỏa mãn yêu cầu bài toán. Chọn đáp án C.
Ví dụ 2: Cho hàm số $f(x)$ có $f(0)=0$ và $f'(x)$ là đa thức bậc bốn có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số $g(x)=left| f(x^3)+x right|$ là
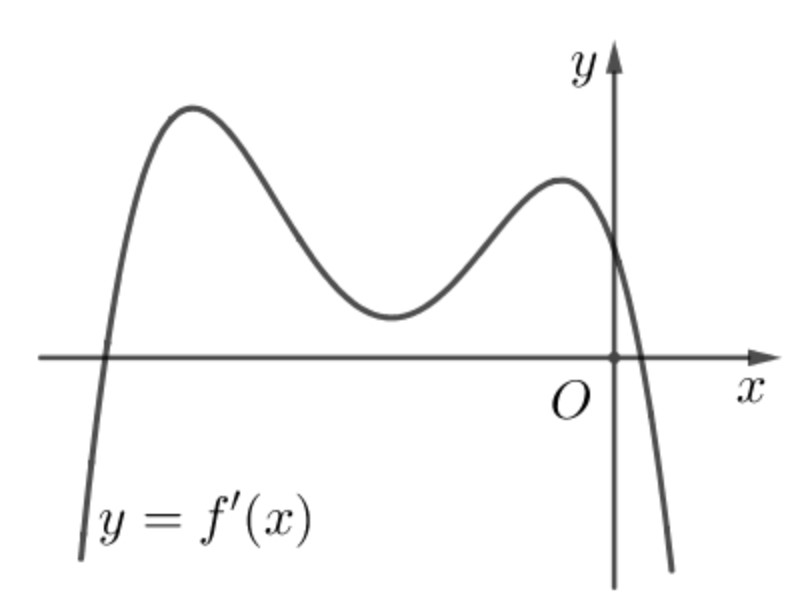
Xét $u=f(x^3)+x$ có $u'=0Leftrightarrow 3x^2f'(x^3)+1=0Leftrightarrow f'(x^3)=-dfrac13x^2.$ Đặt $t=x^3Leftrightarrow x=sqrt[3]t,$ phương trình trở thành: [f'(t)=-dfrac13sqrt[3]t^2(1).] Xét hàm số $y=-dfrac13sqrt[3]x^2$ có $y'=dfrac29sqrt[3]x^5.$ Bảng biến thiên:
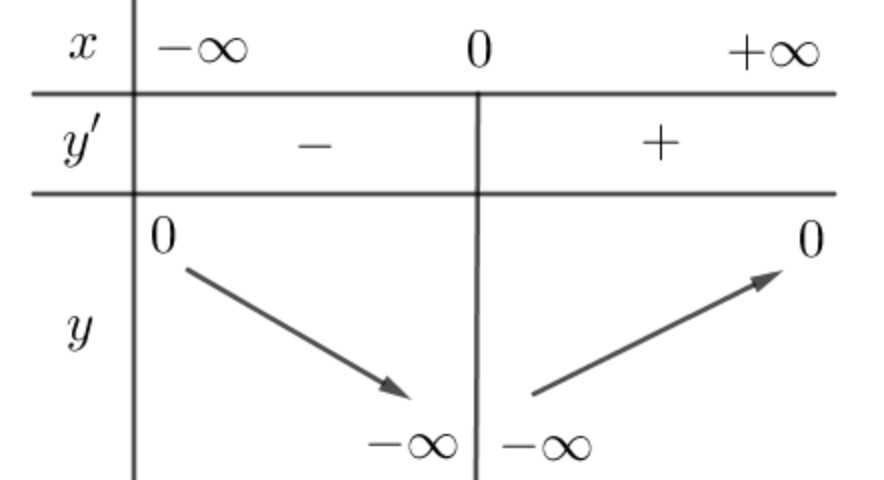
Suy ra đồ thị hàm số $y=-dfrac13sqrt[3]x^2$ được vẽ cùng với đồ thị $f'(x)$ có dạng như hình vẽ bên:
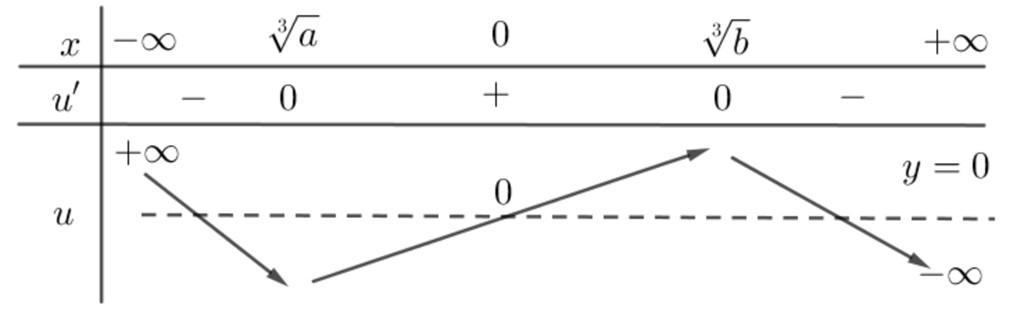
Hai đường cong $f'(x)$ và $y=-dfrac13sqrt[3]x^2$ cắt nhau tại hai điểm phân biệt có hoành độ $a<0 Bảng biến thiên: trong đó $u(0)=f(0)=0.$ Vì vậy hàm số $g(x)=left| u right|$ có tất cả $2+3=5$ điểm cực trị. Chọn đáp án B. Bài tập tự luyện: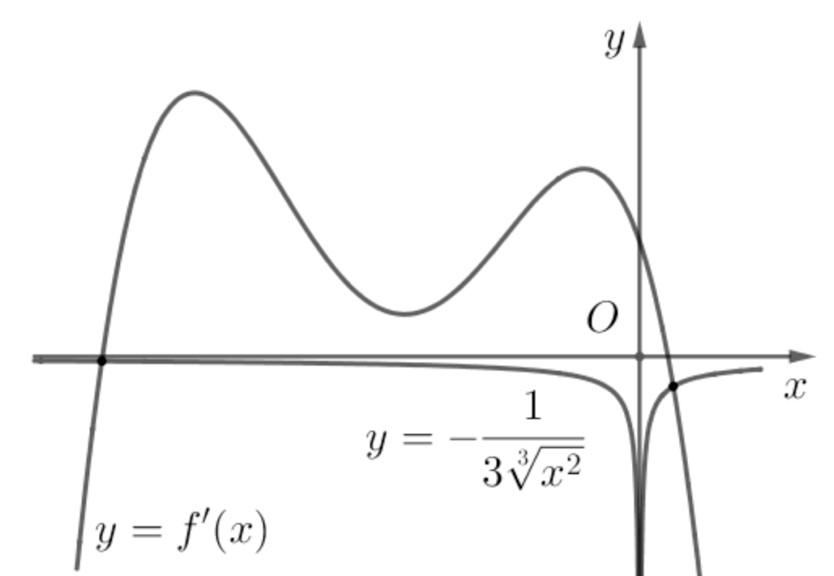


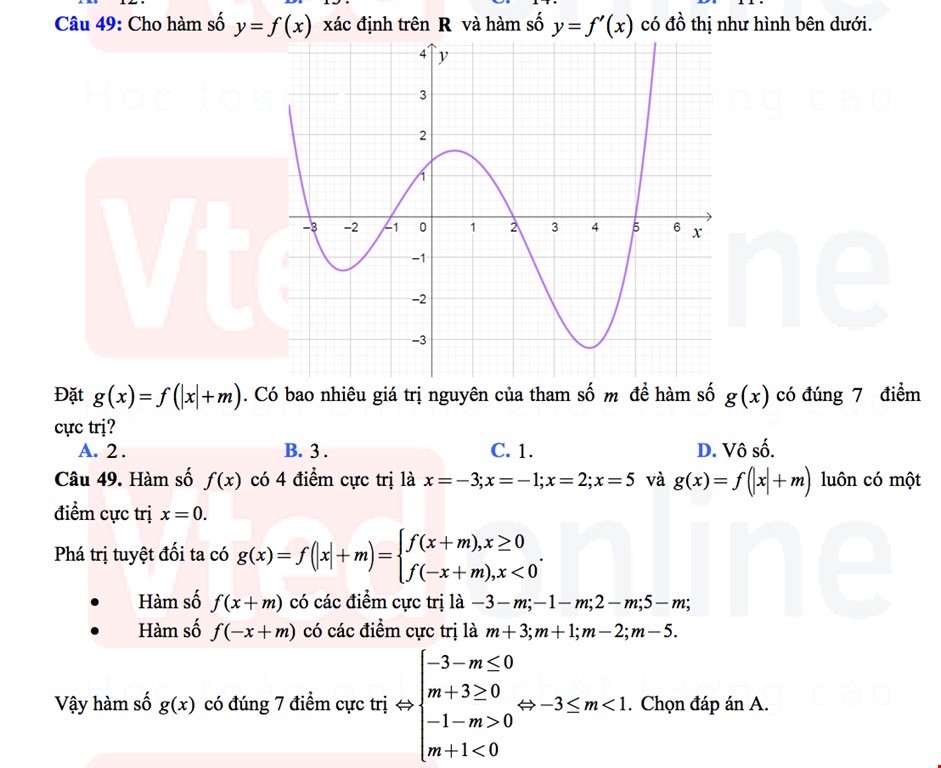
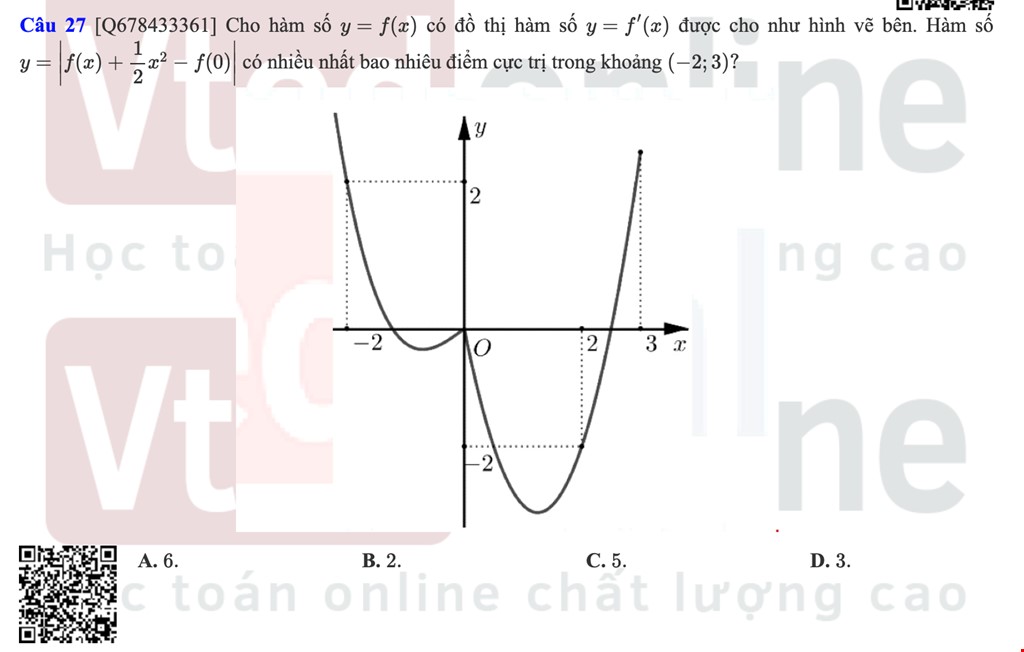




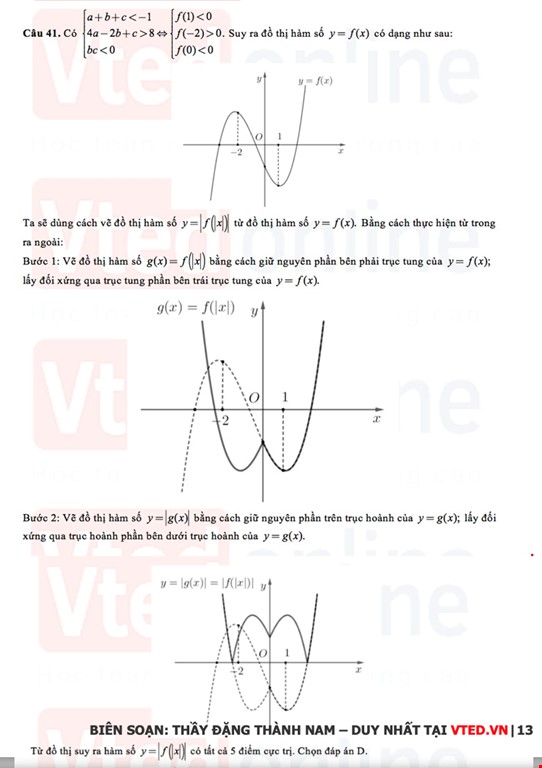
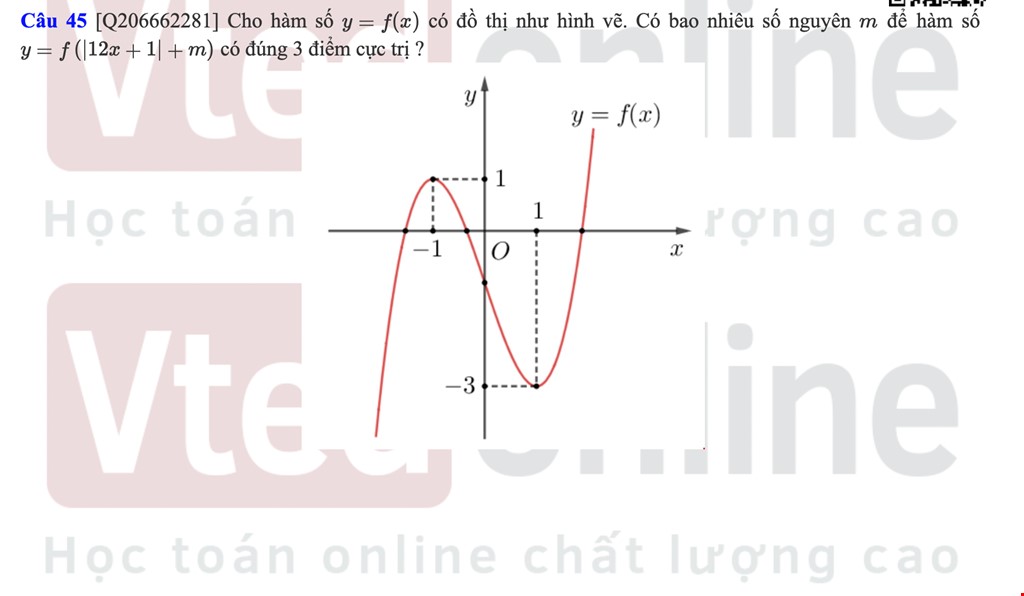


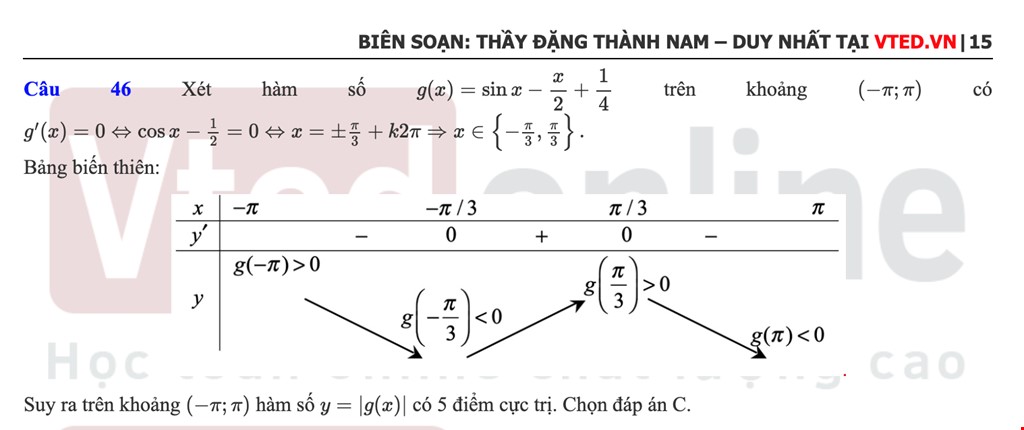













Tuyển tập Đề thi thử Toán THPT Quốc gia 2022 có lời giải rõ ràng
Tải thêm tài liệu liên quan đến nội dung bài viết Hàm số f(x)=x^4 x+1 2 có bao nhiêu điểm cực trị
Review Hàm số f(x)=x^4 x+1 2 có bao nhiêu điểm cực trị ?
Bạn vừa Read nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Review Hàm số f(x)=x^4 x+1 2 có bao nhiêu điểm cực trị tiên tiến nhất
Chia Sẻ Link Download Hàm số f(x)=x^4 x+1 2 có bao nhiêu điểm cực trị miễn phí
Pro đang tìm một số trong những Chia Sẻ Link Down Hàm số f(x)=x^4 x+1 2 có bao nhiêu điểm cực trị Free.
Hỏi đáp thắc mắc về Hàm số f(x)=x^4 x+1 2 có bao nhiêu điểm cực trị
Nếu sau khi đọc nội dung bài viết Hàm số f(x)=x^4 x+1 2 có bao nhiêu điểm cực trị vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha
#Hàm #số #fxx4 #có #bao #nhiêu #điểm #cực #trị

Post a Comment