Review Cho hình chóp sabc có SA = 1, SB = 2, SC = 3
Kinh Nghiệm Hướng dẫn Cho hình chóp sabc có SA = 1, SB = 2, SC = 3 Chi Tiết
Lê Nguyễn Hà Linh đang tìm kiếm từ khóa Cho hình chóp sabc có SA = 1, SB = 2, SC = 3 được Update vào lúc : 2022-07-27 16:56:02 . Với phương châm chia sẻ Bí kíp Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha.Chọn A
Trên cạnh SB, SC lần lượt lấy những điểm M, N thỏa mãn SM = SN = 1.
Ta có AM = 1, AN = 2, MN = 3
=> tam giác AMN vuông tại A
Hình chóp S.AMN có SA = SM = SN = 1.
=> hình chiếu của S trên (AMN) là tâm I của đường tròn ngoại tiếp tam giác AMN, ta có I là trung điểm của MN
Trong ∆SIM, 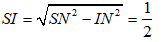
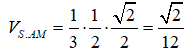
Ta có 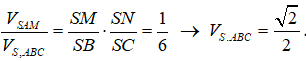
Cho hình chóp S.ABC có SA = 1, SB = 2, SC = 3 và $widehatASB=60^0, widehatBSC=120^0, widehatCSA=90^0$. Tính thể tích khối chóp S.ABC
$fracsqrt26$
$fracsqrt24$
- Hướng dẫn giải
Chọn A
Trên cạnh SB, SC lần lượt lấy những điểm M, N thỏa mãn SM = SN = 1.
Ta có AM = 1, AN = 2, MN = 3
=> tam giác AMN vuông tại A
Hình chóp S.AMN có SA = SM = SN = 1.
=> hình chiếu của S trên (AMN) là tâm I của đường tròn ngoại tiếp tam giác AMN, ta có I là trung điểm của MN
Trong ∆SIM, 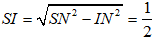
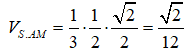
Ta có 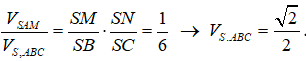
Phương pháp giải:
+) Gọi (B' in SB) ; (C' in SC) sao cho (SA = SB' = SC' = 1).
+) Tính thể tích khối chóp S.AB’C’.
+) Sử dụng công thức tỉ số thể tích.
Lời giải rõ ràng:
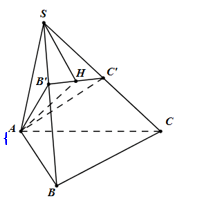
Gọi (B' in SB) ; (C' in SC) sao cho (SA = SB' = SC' = 1).
Xét (Delta SAB') có (left{ beginarraylSA = SB'\angle ASB' = 60^0endarray right. Rightarrow Delta SAB') đều ( Rightarrow AB' = SA = 1).
Xét (Delta SAC') có (widehat S = 90^0 Rightarrow AC' = sqrt SA^2 + SC'^2 = sqrt 2 ).
Xét (Delta SB'C') có : (B'C' = sqrt 1^2 + 1^2 - 2.1.1dfrac - 12 = sqrt 3 ) (Định lí Cosin)
Do đó theo định lí Pytago đảo ta có (Delta AB'C') vuông tại A.
Chóp S.AB’C’ có (SA = SB' = SC') nên hình chiếu của S lên (AB’C’) trùng với tâm đường tròn ngoại tiếp (Delta AB'C'). Mà (Delta AB'C') vuông tại A nên tâm đường tròn ngoại tiếp là trung điểm H của B’C’ ( Rightarrow SH bot left( AB'C' right)).
Xét (Delta SHB') vuông tại H : (SH = SB'.cos 60^0 = dfrac12). Có (S_Delta AB'C' = dfrac12AB'.AC' = dfrac12.1.sqrt 2 = dfracsqrt 2 2). Do đó (V_S.AB'C' = dfrac13SH.S_Delta AB'C' = dfrac13.dfrac12.dfracsqrt 2 2 = dfracsqrt 2 12).
Ta có : (dfracV_S.AB'C'V_S.ABC = dfracSB'SB.dfracSC'SC = dfrac12.dfrac13 = dfrac16 Rightarrow V_S.ABC = 6V_S.AB'C' = dfracsqrt 2 2).
Chọn A.
Cho hình chóp S.ABC có (SA = 1;,,SB = 2;,,SC = 3) và (widehat ASB = 60^0;,,widehat BSC = 120^0;,,widehat CSA = 90^0). Tính thể tích khối chóp S.ABC.
A.
(dfracsqrt 2 2)
B.
C.
(dfracsqrt 2 6)
D.
(dfracsqrt 2 4)
Bằng cách đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách Bảo mật của chúng tôi.

Post a Comment