Review Bài tập sách giáo khoa phương trình mũ và lôgarit
Mẹo Hướng dẫn Bài tập sách giáo khoa phương trình mũ và lôgarit Mới Nhất
Dương Khoa Vũ đang tìm kiếm từ khóa Bài tập sách giáo khoa phương trình mũ và lôgarit được Update vào lúc : 2022-07-20 09:08:01 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Ad lý giải và hướng dẫn lại nha.
 Nội dung chính
Nội dung chính - Website này đang không thể truy cập do dịch vụ Hosting tại AZDIGI bị tạm khóa do quá hạn thanh toán hoặc vi phạm quy định sử dụng dịch vụ. Nếu bạn đã thanh toán và vẫn còn thấy thông báo này, hãy thử xóa cookie/cache của trình duyệt và thử lại. Nếu bạn nhận định rằng đây là lỗi hoặc nhầm lẫn, hãy gửi yêu cầu đến Bộ phận kỹ thuật của AZDIGI tại đây để được tương hỗ nhanh nhất có thể. Mục tiêu bài học kinh nghiệm tay nghề Phương trình mũ và phương trình LogaritLý thuyết cần nắm bài Phương trình mũ và phương trình LogaritI. Phương trình mũII. Phương trình logaritTrả lời thắc mắc Toán 12 Giải tích Bài 5 trang 80Trả lời thắc mắc Toán 12 Giải tích Bài 5 trang 81Trả lời thắc mắc Toán 12 Giải tích Bài 5 trang 83Lời kết sau bài học kinh nghiệm tay nghề Phương trình mũ và phương trình LogaritVideo liên quan
Website này đang không thể truy cập do dịch vụ Hosting tại AZDIGI bị tạm khóa do quá hạn thanh toán hoặc vi phạm quy định sử dụng dịch vụ. Nếu bạn đã thanh toán và vẫn còn thấy thông báo này, hãy thử xóa cookie/cache của trình duyệt và thử lại. Nếu bạn nhận định rằng đây là lỗi hoặc nhầm lẫn, hãy gửi yêu cầu đến Bộ phận kỹ thuật của AZDIGI tại đây để được tương hỗ nhanh nhất có thể.

Tiếp nối với bài học kinh nghiệm tay nghề trước, bài học kinh nghiệm tay nghề ngày hôm nay những em sẽ được học thêm một phần kiến thức và kỹ năng về logarit. Phương trình mũ và phương trình logarit, một dạng bài với nhiều cách thức giải sẽ được Toppy khối mạng lưới hệ thống lại ngay dưới đây cùng những bài tập và cách giải giúp những em dễ hiểu và vận dụng làm được những bài tập khác. Cùng đến với bài học kinh nghiệm tay nghề ngay thôi!
Mục tiêu bài học kinh nghiệm tay nghề Phương trình mũ và phương trình Logarit
- Sau khi tham gia học xong những bài học kinh nghiệm tay nghề này, những bạn nhỏ cần nắm được những kiến thức và kỹ năng, kĩ năng sau:
Nắm vững cách giải những phương trình mũ và logarit cơ bản.
Hiểu rõ những phương pháp thường dùng để giải phương trình mũ và phương trình logarit.
Vận dụng thành thạo những phương pháp giải phương trình mũ và phương trình logarit vào bài tập.
Biết sử dụng những phép biến hóa đơn giản về lũy thừa và logarit vào giải phương trình.
Lý thuyết cần nắm bài Phương trình mũ và phương trình Logarit
Sau đây là những lý thuyết trọng tâm nhất được itoan biên soạn, giúp những bạn nắm vững bài học kinh nghiệm tay nghề và tạo nền tảng giúp những bạn học viên áp dụng giải những bài tập:
I. Phương trình mũ
1. Phương trình mũ cơ bảnĐịnh nghĩa
Phương trình mũ cơ bản có dạng ax=b (a>0,a≠1).
Cách giải
Phương trình: ax=b (a>0,a≠1)
b>0 Có nghiệm duy nhất x=logab
b≤0 Vô nghiệm
Ví dụ: Giải phương trình: 32x=9 .
Giải
Ta có: 32x=9 ⇔ 9x=9 ⇔ x=log99⇔ x=1
Vậy x=1 là nghiệm của phương trình.
2. Cách giải một số trong những phương trình mũ đơn giảna. Đưa về cùng cơ số
Phương pháp:
Bước 1: Biến đổi những lũy thừa về cùng cơ số.
Bước 2: Sử dụng kết quả af(x)=ag(x)⇔f(x)=g(x) (0 Bước 3: Giải phương trình f(x)=g(x) và kết luận. b. Đặt ẩn phụ Bước 1: Tìm một lũy thừa chung đặt làm ẩn phụ và tìm điều kiện cho ẩn. Bước 2: Giải phương trình chứa ẩn phụ, kiểm tra điều kiện. Bước 3: Thay ẩn phụ và giải phương trình đối với ẩn ban đầu. Bước 4: Kết luận nghiệm. c. Lôgarit hóa Khi giải phương trình af(x)=bg(x) (0 Bước 1: Tìm điều kiện xác định. Bước 2: Lấy logarit cơ số a (hoặc b) hai vế. Bước 3: Giải phương trình. Bước 4: Kết luận Phương trình lôgarit là phương trình có chứa ẩn số trong biểu thức dưới dấu lôgarit. Ví dụ: log2(x2+2x+3)=4 là một phương trình logarit. Phương trình logarit cơ bản có dạng: logax=b (0 Theo định nghĩa Lôgarit ta có: logax = b ⇔ x=ab. Kết luận: Phương trình logax=b (0 a. Đưa về cùng cơ số Phương pháp: Bước 1: Biến đổi những lôgarit về cùng cơ số. Bước 2: Sử dụng kết quả logaf(x)=logag(x) ⇔ f(x)=g(x) (0 Bước 3: Giải phương trình f(x)=g(x) và kết luận. b. Đặt ẩn phụ Bước 1: Tìm một lũy thừa chung đặt làm ẩn phụ và tìm điều kiện cho ẩn. Bước 2: Giải phương trình chứa ẩn phụ, kiểm tra điều kiện. Bước 3: Thay ẩn phụ và giải phương trình đối với ẩn ban đầu. Bước 4: Kết luận nghiệm. c. Mũ hóa Khi giải phương trình logaf(x)=g(x) (0 Bước 1: Tìm điều kiện xác định. Bước 2: Mũ hóa cơ số a hai vế. Bước 3: Giải phương trình. Bước 4: Kết luận Bài học này quá nhiều lý thuyết quan trọng đúng không nào, những bạn hoàn toàn có thể phối hợp học lý thuyết cùng video hướng dẫn dưới đây để nắm chắc kiến thức và kỹ năng hơn nhé! Phần bài tập trong sách giáo khoa rất sát với lý thuyết nên những bạn nỗ lực hoàn thành xong hết nhé! Giải phương trình 6(2x – 3) = 1 bằng phương pháp đưa về dạng aA(x) = aB(x) và giải phương trình A(x) = B(x). Hướng dẫn giải: 6(2x – 3) = 1 ⇔ 6(2x – 3) = 60 ⇔ 2x – 3 = 0 ⇔ x = 3/2. Đặt t = 5x, ta có (1)⇔ 1/5.t2 + 5t = 250 ⇔ t2 + 25t – 1250 = 0 ⇔ t = 25 hoặc t = -50(loại) ⇔ 5x ⇔ x = 2. Tính x, biết log3x = 1/4. Hướng dẫn giải: Theo định nghĩa logarit ta có x = 31/4. log9x = log32x = 1/2 log3x. Vây phương trình đã cho tương đương với phương trình: log3x + 1/2 log3x = 6. Với t = log2x. Ta có phương trình đã cho tương đương với phương trình: Giải phương trình log1/2x + (log2x)2 = 2. Hướng dẫn giải: Giải những phương trình mũ: Hướng dẫn giải: Giải những phương trình mũ: Hướng dẫn giải Giải những phương trình logarit: Hướng dẫn giải: Giải phương trình: Hướng dẫn giải: Sau khi tham gia học xong phương trình mũ và phương trình logarit những em đã hiểu được định nghĩa và những phương pháp giải của phương trình chưa nào? Nếu chưa hiểu phần kiến thức và kỹ năng nào những em hãy phản hồi phía phía dưới để những thầy cô Toppy hướng dẫn giải đáp ngay nhé! Ngoài ra, những bạn hoàn toàn có thể truy cập vào trang web Toppy để rèn luyện những bài tập khác từ cơ bản đến nâng cao cùng những bài học kinh nghiệm tay nghề khác. Toppy là công ty Edtech về giáo dục trực tuyến, đáp ứng trải nghiệm học tập thành viên cho hàng trăm nghìn học viên, sinh viên và nhà trường để giải đáp những yêu cầu trong việc học tập thông qua mạng lưới những Chuyên Viên và giáo viên khắp toàn cầu mà Toppy gọi là những gia sư học thuật quốc tế. Với kho tàng kiến thức và kỹ năng khổng lồ theo từng chủ đề, bám sát chương trình sách giáo khoa, những thầy cô Toppy luôn nỗ lực mang lại cho những em những bài giảng hay, dễ hiểu nhất, giúp những em tiến bộ hơn từng ngày. Chúc những bạn sẽ thành công trong việc làm chủ môn Giải tích 11 và đạt thật nhiều điểm thưởng. II. Phương trình logarit
Trả lời thắc mắc Toán 12 Giải tích Bài 5 trang 80
Trả lời thắc mắc Toán 12 Giải tích Bài 5 trang 81
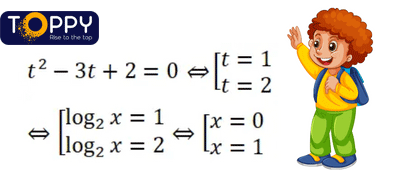 phương trình mũ và phương trình logarit
phương trình mũ và phương trình logarit
Trả lời thắc mắc Toán 12 Giải tích Bài 5 trang 83
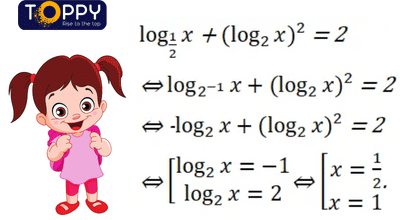

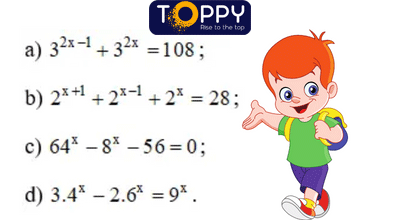


Lời kết sau bài học kinh nghiệm tay nghề Phương trình mũ và phương trình Logarit
Clip Bài tập sách giáo khoa phương trình mũ và lôgarit ?
Bạn vừa đọc nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Video Bài tập sách giáo khoa phương trình mũ và lôgarit tiên tiến nhất
Share Link Down Bài tập sách giáo khoa phương trình mũ và lôgarit miễn phí
Heros đang tìm một số trong những Share Link Down Bài tập sách giáo khoa phương trình mũ và lôgarit miễn phí.
Giải đáp thắc mắc về Bài tập sách giáo khoa phương trình mũ và lôgarit
Nếu sau khi đọc nội dung bài viết Bài tập sách giáo khoa phương trình mũ và lôgarit vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Admin lý giải và hướng dẫn lại nha
#Bài #tập #sách #giáo #khoa #phương #trình #mũ #và #lôgarit

Post a Comment