Mẹo Cho hình chóp sabc có M là trung điểm SA
Thủ Thuật Hướng dẫn Cho hình chóp sabc có M là trung điểm SA Mới Nhất
Cao Ngọc đang tìm kiếm từ khóa Cho hình chóp sabc có M là trung điểm SA được Update vào lúc : 2022-07-13 11:22:02 . Với phương châm chia sẻ Bí kíp Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tham khảo nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Admin lý giải và hướng dẫn lại nha.
- lý thuyết trắc nghiệm hỏi đáp bài tập sgk
Cho hình chóp SABC , có M là trung điểm của SA. Mặt phẳng qua M và song song với mp (ABC) cắt CB tại N, cắt SC tại P. Tính:
a) tỉ số thể tích giữa SMNP và SABC
b)tỉ số thể tích giữa SMNP và SAMN
Các thắc mắc tương tự
Cho hình chóp tứ giác đều S. ABCD, M là trung điểm của SC. Mặt phẳng (P) qua AM và song song với BD cắt SB, SD tại N, K. Tính tỉ số thể tích của khối S. ANMK và khối chóp S.ABCD.
A. 2 9
B. 1 3
C. 1 2
D. 3 5
Cho khối chóp S.ABC. Gọi G là trọng tâm của tam giác SBC. Mặt phẳng (α) qua AG và song song với BC cắt SB,SC lần lượt tại I,J. Tính tỉ số thể tích của hai khối tứ diện SAIJ và SABC.
A. 1 9 .
B. 4 9 .
C. 1 3 .
D. 2 3 .
Cho tứ diện SABC và hai điểm M, N lần lượt thuộc những cạnh SA, SB sao cho S M A M = 1 2 , S N B N = 2 . Mặt phăng (P) đi qua hai điểm M, N và song song với cạnh SC, cắt AC, BC lần lượt tại L, K. Tính tỉ số thể tích V S C M N K L V S A B C
A. V S C M N K L V S A B C = 4 9
B. V S C M N K L V S A B C = 1 3
C. V S C M N K L V S A B C = 2 3
D. V S C M N K L V S A B C = 1 4
Cho hình chóp S.ABCD. Trên cạnh SA lấy điểm M sao cho SM = 1 3 SA . Mặt phẳng α qua M và song song với mặt đáy lần lượt cắt SB, SC, SD tại N, P, Q.. Tỉ số thể tích của khối chóp S.MNPQ với khối chóp S.ABCD là
A. 1 9
B. 1 3
C. 1 81
D. 1 27
Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông vắn cạnh a, cạnh bên tạo với đáy một góc 60 o . Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD, cắt SB tại P và cắt SD tại Q.. Thể tích khối chóp S.AMNQ là V. Tỉ số 18 V a 3 là ?
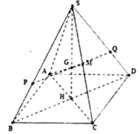
A. 2
B. 6
C. 3
D. 1
Cho hình chóp S.ABC. Gọi α là mặt phẳng đi qua A và song song với BC. Mặt phẳng α cắt SB, SC lần lượt tại M, N. Tính tỉ số S M S B biết α chia khối chóp thành 2 phần hoàn toàn có thể tích bằng nhau
A. 1/2
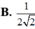
C. 1/3
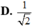
Cho hình chóp SABC có đáy ABC là tam giác vuông tại A, cạnh A B = 2 , A B C ^ = 60 ° . Hình chiếu vuông góc của S trên mặt phẳng đáy là trung điểm M của BC, góc giữa SA và mặt đáy bằng 45 ° . Tính thể tích V của khối chóp SABC.
A. V = 4 3 3
B. V = 4 3
C. V = 2 3
D. V = 2
Cho khối chóp (S.ABC), gọi (M) là trung điểm của (SA). Chọn xác định sai trong những xác định sau:
A.
Khối chóp S.ABC có 4 mặt đều là tam giác
B.
(V_S.MBC = V_M.ABC)
C.
(V_S.ABC = 2V_M.ABC)
D.
(V_S.MBC over V_S.ABC = 2 over 3)
Cho hình chóp (S.ABC ), gọi (M ) là trung điểm (SB ) và (N ) là vấn đề thuộc cạnh (SC ) sao cho (SN = 2NC ). Tính tỉ số ( dfracV_S.AMNV_S.ABC )
A.
(dfracV_S.AMNV_S.ABC = dfrac13)
B.
(dfracV_S.AMNV_S.ABC = dfrac23)
C.
(dfracV_S.AMNV_S.ABC = 2)
D.
(dfracV_S.AMNV_S.ABC = dfrac12)
Phương pháp giải:
Công thức tính thể tích khối chóp có diện tích s quy hoạnh đáy (S) và độ cao (h) là: (V = dfrac13Sh.)
Lời giải rõ ràng:
Ta có: (dfracV_M.ABCV_S.ABC = dfracdfrac13dleft( M,,,left( ABC right) right).S_ABCdfrac13dleft( S,,,left( ABC right) right).S_ABC = dfracdleft( M,,,left( ABC right) right)dleft( S,,,left( ABC right) right) = dfracMASA = dfrac12.)
Chọn A.
Cho hình chóp $S.ABC$. Gọi $M$ là trung điểm của $SA$ và $N$ là vấn đề trên $SC$ sao cho $SN=2NC$. Tính tỷ số $k$ giữa thể tích khối chóp $ABMN$ và thể
Cho hình chóp (S.ABC). Gọi (M) là trung điểm của (SA) và (N) là vấn đề trên (SC) sao cho (SN = 2NC). Tính tỷ số (k) giữa thể tích khối chóp (ABMN) và thể tích khối chóp (S.ABC.)
A. (dfrac23.)
B. (dfrac13.)
C. (dfrac14.)
D. (dfrac25.)
Phương pháp
Công thức tính thể tích khối chóp có diện tích s quy hoạnh đáy S và độ cao h là: V = 13Sh
Cách giải:
Ta có:
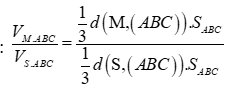
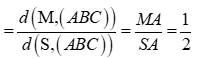
Chọn A.

Post a Comment